Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 176

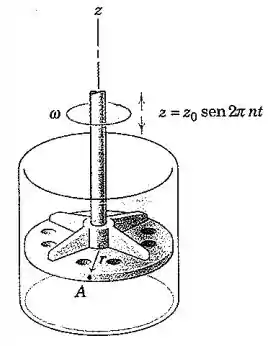
O elemento giratório em uma câmara de mistura recebe um movimento axial periódico z = z 0   s e n 2 π n t enquanto está girando na velocidade angular constante θ ˙ = ω . Determine a expressão para o módulo máximo da aceleração de um ponto A sobre a borda de raio r . A frequência n da oscilação vertical é constante.

Passo 1

Galera, lembra que a aceleração em coordenadas cilíndricas é assim?

a = r ¨ - r θ ˙ 2   e r + r θ ¨ + 2 r ˙ θ ˙   e θ + z ¨   k

Pois então, vamos usar justamente essa fórmula aí, calculando cada componente.

Como o ponto A tem raio r constante, e a velocidade angular θ ˙ = ω é constante, temos o seguinte:

r ˙ = r ¨ = θ ¨ = 0

Então, já podemos calcular as duas primeiras componentes da aceleração:

a r = r ¨ - r θ ˙ 2 = 0 - r ω 2 = - r ω 2

a θ = r θ ¨ + 2 r ˙ θ ˙ = 0 + 0 = 0

Passo 2

A componente que ainda falta determinar é:

a z = z ¨

Ou seja, é a segunda derivada de z em relação ao tempo t . Porém, o exercício já nos deu a expressão de z em função de t , então só temos que derivar:

z = z 0   s e n 2 π n t

z ˙ = z 0 2 π n cos ⁡ 2 π n t

z ¨ = z 0 2 π n 2 - s e n 2 π n t = - 4 π 2 n 2 z 0   s e n 2 π n t

Portanto,

a z = - 4 π 2 n 2 z 0   s e n 2 π n t

Passo 3

Enfim, podemos achar uma expressão para o módulo da aceleração, que depende do tempo t :

a = a r 2 + a θ 2 + a z 2 = - r ω 2 2 + 0 2 + - 4 π 2 n 2 z 0   s e n 2 π n t 2

a t = r 2 ω 4 + 16 π 4 n 4 z 0 2   s e n 2 2 π n t

Note que a aceleração máxima vai ocorrer quando s e n 2 2 π n t = 1 , então:

a m á x = r 2 ω 4 + 16 π 4 n 4 z 0 2

Resposta

a m á x = r 2 ω 4 + 16 π 4 n 4 z 0 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade de uma partícula é dada por v = 16 t 2 i + 4 t 3 j + 5 t + 2 k m/s, onde t é dado em segundos. Se a partícula está na origem quando t = 0 , determine a intensidade da aceleração da partíc
Uma partícula move-se ao longo da trajetória y 2 = 4 x com uma velocidade escalar constante de v = 4 m / s . Determine as componentes x e y da velocidade e aceleração quando a partícula está em x = 4
A velocidade de uma partícula é v = 3 i + 6 - 2 t j m / s , onde t é dado em segundos. Se r = 0 quando t = 0 , determine o deslocamento da partícula durante o intervalo de tempo t = 1 s a t = 3 s .
Uma caixa deslizando encosta abaixo, como descrito pela equação y = ( 0.05 x 2 ) m, onde x é dado em metros. Se a caixa tem componentes x de velocidade e aceleração com v x = - 3 m / s e a x = - 1.5m
A posição de uma partícula é r = 3 t 2 - 2 t i - 4 t 1 / 2 + t j + 3 t 2 - 2 k m , onde t é dado em segundos. Determine a intensidade da velocidade e da aceleração da partícula quando t = 2 s