Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 85

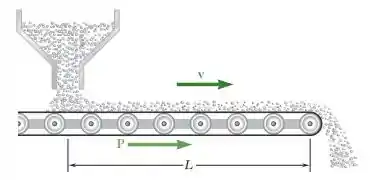
O cascalho cai com velocidade zero em um transportador de correia com a taxa q = d m / d t   constante. ( a )   Determine a intensidade da força P necessária para manter a velocidade da correia v constante. ( b )   Mostre que a energia cinética adquirida pelo cascalho em um dado intervalo de tempo é igual à metade do trabalho realizado no intervalo pela força P . Explique o que acontece com a outra metade do trabalho feito pela força P .

Passo 1

Fala aí, galerinha. Tudo certo? Bora para mais uma questãozinha de Dinâmica. Primeiro, temos que determinar a intensidade da força P necessária para manter a velocidade da correia v constante.

Para isso, vamos aplicar o princípio que relaciona o impulso e o momento linear em relação ao cascalho na correia e à massa ∆ m de cascalho que atinge e sai da correia no intervalo ∆ t :

m v + P ∆ t = m v + ∆ m v P = ∆ m ∆ t v

Podemos observar que ∆ m / ∆ t corresponde a taxa q que o enunciado nos fala. Logo:

P = q v

Opa, encontramos a força P . Bora pra segunda parte do exercício.

Passo 2

Em seguida, temos que mostrar que a energia cinética adquirida pelo cascalho em um dado intervalo de tempo é igual à metade do trabalho realizado no intervalo pela força P . Sabemos que a energia cinética por unidade de tempo é dada por:

∆ T = 1 2 ∆ m v 2

Vamos dividir a equação por ∆ t . Temos:

∆ T ∆ t = 1 2 ∆ m ∆ t v 2 ∆ T ∆ t = 1 2 q v 2                                       1

E também, sabemos que o trabalho pela unidade de tempo realizado pela força P é dado por:

∆ U ∆ t = P ∆ x ∆ t

Substituindo pela força P que a gente encontrou no passo anterior, temos

∆ U ∆ t = q v ∆ x ∆ U ∆ t = q v v = q v 2                                       2

Comparando as duas relações que a gente encontrou, temos:

∆ T ∆ t = 1 2 q v 2

Conseguimos mostrar o que foi pedido.

Para a outra metade do trabalho da força P , ela é dissipada em calor por fricção quando o cascalho desliza na correia antes de atingir a velocidade v .

É isso, galerinha. Bora praticar mais pra ficar craque!

Resposta

P = q v

∆ T ∆ t = 1 2 q v 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um homem de 90 kg e uma mulher de 60 kg estão lado a lado na mesma extremidade de um barco de 150 kg, prontos para mergulhar, cada um com uma velocidade de 5 m/s em relação ao barco. Determine a veloc
Um sistema consiste de três partículas,A,BeC. Sabemos quemA= 3 kg,mB= 4 kg emC= 5 kg e que as velocidades das partículas, expressas em m/s, são respectivamente,vA= − 4i+ 4j+ 6k,vB=vxi+vyj+ 4kevC= 2i−
Em um parque de diversões há carros bate-bateA,BeCde 200 kg com pilotos com massas de 40 kg, 60 kg e 35 kg respectivamente. O carroAestá se movendo para a direita com a velocidadevA= 2 m/s e o carroCt
Observa-se um pequeno avião de 1.500 kg de peso e um helicóptero de 3.000 kg de peso voando a uma altitude de 1.200 m preste a colidir diretamente acima de uma torre localizada emOem uma área arboriza
Um sistema consiste de três partículas,A,BeC. Sabemos quemA= 3 kg,mB= 4 kg emC= 5 kg e que as velocidades das partículas, expressas em m/s, são respectivamente,vA= − 4i+ 4j+ 6k,vB=vxi+vyj+ 4kevC= 2i−