Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 28
2.28. A viga deve ser içada usando-se duas correntes. Determine as intensidades das forças que atuam em cada corrente, a fim de obter uma força resultante de orientada ao longo do eixo y positivo. Considere .
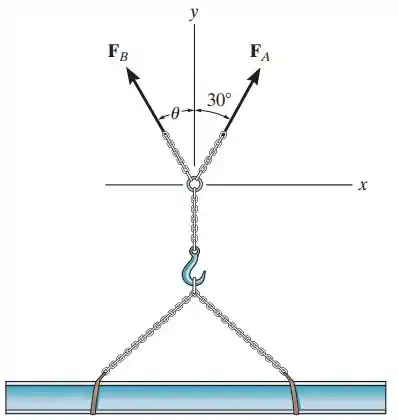
Passo 1
Vamos analisar os vetores , e como vetores, e aí poderemos usar a lei dos paralelogramos, vou desenhar isso.
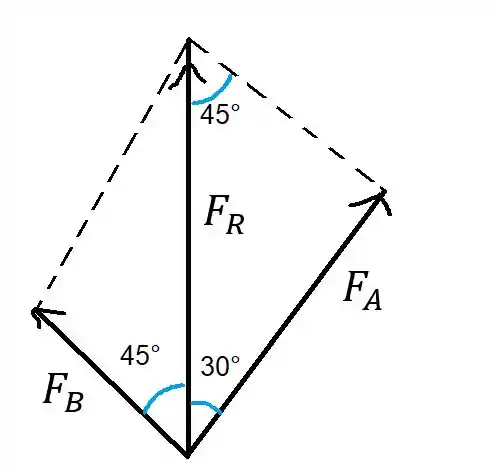
Daqui podemos extrair o seguinte triângulo
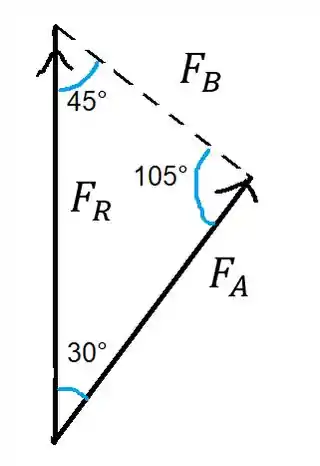
Passo 2
Para determinar a intensidade das forças podemos usar a lei dos senos
Passo 3
Agora vamos calcular para
Resposta
Exercícios de Livros Relacionados
Para os vetores V 1 e V 2 do Prob. ½, determine o módulo da diferença vetorial V ' = V 2 - V 1 e o ângulo θ x que V ' faz com o eixo positivo x . Complete tanto a solução gráfica quanto a algébrica.
Determine os ângulos feitos pelo vetor V = - 36i + 15j com o eixo positivo dos x e dos y . Escreva o vetor unitário n na direção de V .
A partir da lei gravitacional calcule o peso W (força gravitacional em relação à Terra) de um homem de 80k g , em uma espaçonave percorrendo uma órbita circular 250k m acima da superfície da Terra. Ex
O elemento de volume Δ V do cone circular de altura h e base de raio r é formado cortando-se um elemento fino do cone a uma distância x do vértice. Se o elemento cortado tiver uma espessura finita Δ x
2.5. Decomponha F 1 em componentes ao longo dos eixos u e v , e determine suas intensidades.