Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 138

15.139. As rodas fixadas às extremidades da barra AB rolam ao longo das superfícies mostradas na figura. Usando o método da Seção 15.9 e sabendo que a aceleração da roda B é zero, deduza uma expressão para a velocidade angular da barra em termos de v B , θ ,   l   e   β

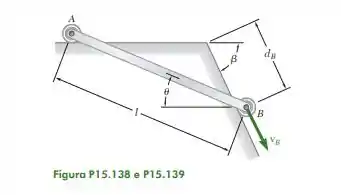
Passo 1

Vamos começar mais uma! A imagem nos dá um triângulo:

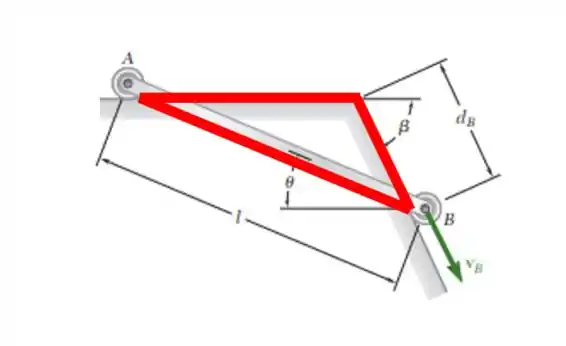
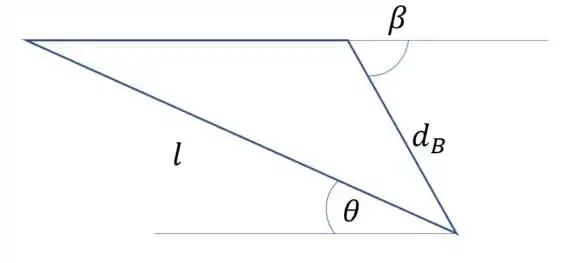
Se a gente usar o teorema de Tales, podemos fazer

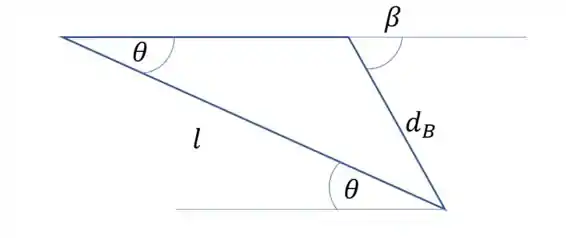
Passo 2

Agora temos um triângulo para trabalhar, vamos usar a lei dos senos

d B sin ⁡ θ = l sin ⁡ β

Então

d B = l sin ⁡ θ sin ⁡ β  

Mas temos que

v B = d d t d B

Então

v B = d d t l sin ⁡ θ sin ⁡ β  

Passo 3

Agora é só resolver essa derivada

v B = d d t l sin ⁡ θ sin ⁡ β  

Vamos começar tirando as constantes

v B = l sin ⁡ β d d t sin ⁡ θ  

Agora vamos usar a regra da cadeia

v B = l sin ⁡ β d d θ sin ⁡ θ   d θ d t  

Isso fica

v B = l sin ⁡ β cos ⁡ θ   ω

Logo

ω = v B sin ⁡ β l cos ⁡ θ

Resposta

ω = v B sin ⁡ β l cos ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra BDE está presa a duas hastes AB e CD. Sabendo que, no instante mostrado na figura, a haste AB gira com uma velocidade angular constante de 3 rad/s no sentido horário, determine a aceleração (a
Um carro C é suportado por um rodízio A e um cilindro B, cada um com 50 mm de diâmetro. Sabendo que no instante mostrado na figura o carro tem uma aceleração de 2,4 m/s² e uma velocidade de 1,5 m/s, a
Um automóvel desloca-se para a esquerda a uma velocidade constante de 80 km/h. Sabendo que o diâmetro da roda é de 500 mm, determine a aceleração (a) do ponto B, (b) do ponto C, (c) do ponto D.
O movimento do cilindro de 75 mm de raio é controlado pela corda mostrada na figura. Sabendo que a extremidade E da corda tem velocidade de 300 mm/s e aceleração de 480 mm/s², ambas orientadas para ci
A barra BDE está presa a duas hastes AB e CD. Sabendo que, no instante mostrado na figura, a haste AB gira com uma velocidade angular constante de 3 rad/s no sentido horário, determine a aceleração (a