Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 111

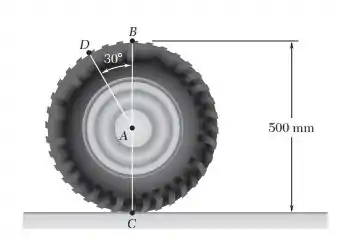
Um automóvel desloca-se para a esquerda a uma velocidade constante de 80 km/h. Sabendo que o diâmetro da roda é de 500 mm, determine a aceleração (a) do ponto B, (b) do ponto C, (c) do ponto D.

Passo 1

Vamos lá resolver mais essa. A velocidade do ponto A, no centro da roda, é igual a velocidade do automóvel, que se movimenta a uma velocidade constante. Assim, a A = 0 . Como a roda não desliza, podemos dizer que é velocidade do ponto C será igual a velocidade do ponto A. Logo,

v A = A C ω

80 3,6 = 0,25 ω → ω = 88,9   r a d / s

Passo 2

A aceleração do ponto B é dada por:

a → B = a → A + a → B / A → a B = r ω 2 = 0,25 ⋅ 88,9 2 = 1975,8   m / s 2

Os outros pontos são obtidos de maneira semelhante:

a → C = a → A + a → C / A → a C = r ω 2 = 0,25 ⋅ 88,9 2 = 1975,8   m / s 2

a → D = a → A + a → D / A → a B = r ω 2 = 0,25 ⋅ 88,9 2 = 1975,8   m / s 2

Resposta

  1. 1975,8 m/s²
  2. 1975,8 m/s²
  3. 1975,8 m/s²
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco deslizante se desloca com uma velocidade v B = 1,5m / s e uma aceleração a B = 0,9m / s 2 . Determine a aceleração de A no instante mostrado.
A manivela AB gira com uma velocidade angular ω A B = 6r a d / s e uma aceleração angular α A B = 2r a d / s 2 . Determine a aceleração de C e a aceleração angular de BC no instante mostrado.
A polia A gira com a velocidade angular e aceleração angular mostradas. Determine a aceleração angular do bloco E no instante mostrado.
A polia A gira com a velocidade angular e aceleração angular mostradas. Determine a aceleração angular da polia B no instante mostrado.
O latão basculante se articula em torno de C e é operado pelo cilindro hidráulico AB. Se o cilindro está estendendo-se a uma taxa constante de 0,15 m/s, determine a velocidade angular ω do latão no in