Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 113

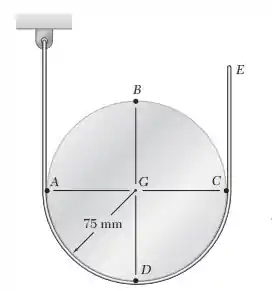
O movimento do cilindro de 75 mm de raio é controlado pela corda mostrada na figura. Sabendo que a extremidade E da corda tem velocidade de 300 mm/s e aceleração de 480 mm/s², ambas orientadas para cima, determine a aceleração (a) do ponto A, (b) do ponto B.

Passo 1

Vamos lá resolver mais essa. Como o ponto E e o ponto C estão na mesma linha de movimento, v C = v E = 300   m m / s . Assim, em relação ao ponto A, temos:

v C = 2 r ω

ω = v C 2 r = 300 2 ⋅ 75 = 2   r a d / s

Disso, podemos calcular a aceleração do ponto C em relação ao ponto A, para obter a aceleração angular do cilindro:

a → C =   a → A + a → C / A

a → C = a C t j → - a C n i → = a E j → - a C n i →

a E j → - a C n i → = a A i → + α k → × 2 r i → - ω 2 2 r i → = a A i → + 2 r α j → - 2 r ω 2 i →

a E = 2 r α → α = 480 2 ⋅ 75 = 3,2   r a d / s 2

Passo 2

Agora, vamos calcular a aceleração do ponto G em relação ao ponto A, em que o ponto G tem o sentido da aceleração apontando para cima. Logo:

a → G =   a → A + a → G / A

a G j → = a A i → + α k → × r i → - ω 2 r i → =   a A i → + ( r α ) j → - ω 2 r i →

a G = 75 ⋅ 3,2 = 240   m m / s 2

a A = 2 2 ⋅ 75 = 300   m m / s 2

Passo 3

Com todos esses dados dos passos anteriores, podemos calcular a aceleração do ponto B:

a → B = a → G j → + α k → × r j → - ω 2 r j → = a → G j → - r α i → - ω 2 r j →

a → B = 240 j → - 240 i → - 300 j →  

a → B =   - 240 i → - 60 j →

a B =   240 2 + 60 2 = 247   m m / s 2

Resposta

  1. 300 mm/s²
  2. 247 mm/s²
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma corda está enrolada em torno da bobina interna da engrenagem. Se ela é puxada com uma velocidade constante v, determine as velocidades e acelerações dos pontos A e B. A engrenagem rola sobre a cre
O disco rola sem deslizar e, em um dado instante, tem o movimento angular mostrado. Determine a velocidade angular e a aceleração angular do membro com ranhura BC nesse instante. O pino em A está fixo
O mecanismo de dois membros serve para amplificar o movimento angular. O membro AB tem um pino em B que está confinado a se deslocar dentro da ranhura do membro CD. Se, no instante mostrado, AB (entra
O cilindro hidráulico está se estendendo com a velocidade e aceleração mostradas. Determine a aceleração angular da manivela AB e do segmento BC no instante mostrado.
O disco rola sem deslizar e, em um dado instante, tem o movimento angular mostrado. Determine a velocidade angular e a aceleração angular do membro com ranhura BC nesse instante. O pino em A está fixo