Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 109

A barra BDE está presa a duas hastes AB e CD. Sabendo que, no instante mostrado na figura, a haste AB gira com uma velocidade angular constante de 3 rad/s no sentido horário, determine a aceleração (a) do ponto D e (b) do ponto E.

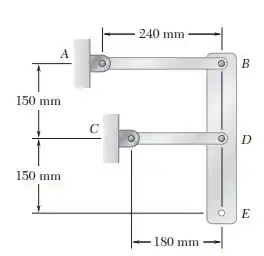
Passo 1

Vamos lá resolver mais essa. A velocidade angular da haste AB, com sentido horário, é ω A B = 3   r a d / s . Assim, vamos assumir que ω C D e ω B D também possuem sentidos horários. Com ω A B , podemos calcular a velocidade do ponto B:

v B = A B ω A B = 0,24 ⋅ 3 = 0,72   m / s   ↓

E para o ponto D, temos:

v D = 0,18 ω C D

v → D = v → B + v → D / B

- 0,18 ω C D j → =   - 0,72   j → - 0,15 ω B D i →

- 0,18 ω C D = 0,72 → ω C D = 4   r a d / s

0,15 ω B D = 0 → ω B D = 0

v D = 0,72     m / s   ↓

Passo 2

Agora vamos fazer uma análise da aceleração em cada barra. Como a velocidade de AB é constante, α A B = 0 . As outras barras possuem aceleração em sentido horário, acompanhando o movimento de AB. A aceleração do ponto D é descrita como:

a → D = a → B + a → D / B t + a → D / B n

Então, podemos escrever cada termo da equação como:

a → B = - α A B k → × A B i → - ω A B 2 A B i → = - 0,24 ⋅ 0 j → - 0,24 ⋅ 3 2 i → = - 2,16   i →

a → D = - α C D k → × C D i → - ω C D 2 C D i → = - 0,18 α C D j → - 0,18 ⋅ 4 2 i → = - 0,18 α C D j → - 2,88 i →

a → D / B t = - α B D k → × ( - B D ) j → = - 0,15 α B D i →

a → D / B n = - ω B D 2 - B D j → = 0 2 ⋅ i → = 0

Substituindo na equação:

- 0,18 α C D j → - 2,88 i → =   - 2,16   i → - 0,15 α B D i →

0,18 α C D = 0 → α C D = 0

2,88 = 2,16 + 0,15 α B D → α B D = 4,8   r a d / s 2  

Passo 3

Com as informações dos passos anteriores podemos descobrir a aceleração do ponto D e do ponto E:

a → D = - 0,18 ⋅ 0 j → - 2,88   i → = - 2,88 i → → a D = 2,88   m / s 2

a → E = a → D + a → E / D t + a → E / D n

a → E / D t = - α D E k → × - D E j → = - 0,15 ⋅ 4,8 i → = - 0,72 i →

a → E / D n = - ω D E 2 - D E j → = 0 2 ⋅ i → = 0

a → E = - 2,88 i → - 0,72 i → = - 3,6   i → → a E = 3,6   m / s 2

Resposta

  1. 2,88 m/s²
  2. 3,6 m/s²
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A argola é lançada na superfície áspera de maneira que ela tem uma velocidade angular ω = 4r a d / s e uma aceleração angular α = 5r a d / s 2 . Além disso, seu centro tem uma velocidade v O = 5m / s
O disco está se deslocando para a esquerda de tal maneira que ele tem uma aceleração angular α = 8r a d / s 2 e velocidade angular ω = 3r a d / s no instante mostrado. Se ele não desliza em A, determi
A argola é lançada na superfície áspera de maneira que ela tem uma velocidade angular ω = 4r a d / s e uma aceleração angular α = 5r a d / s 2 . Além disso, seu centro tem uma velocidade v O = 5m / s
A barra AB tem o movimento angular mostrado. Determine a aceleração do anel C nesse instante.
No instante mostrado, o bloco deslizante B está se deslocando para a direita com a velocidade e aceleração mostradas. Determine a aceleração angular da roda nesse instante.