Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 112

Um carro C é suportado por um rodízio A e um cilindro B, cada um com 50 mm de diâmetro. Sabendo que no instante mostrado na figura o carro tem uma aceleração de 2,4 m/s² e uma velocidade de 1,5 m/s, ambas orientadas para a esquerda, determine (a) a aceleração do rodízio e do cilindro, (b) as acelerações dos centros do rodízio e do cilindro.

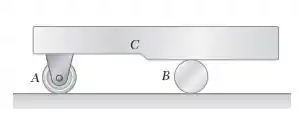
Passo 1

Vamos lá resolver mais essa. Inicialmente, podemos afirmar que a A = a C = 2,4   m / s 2 . Agora vamos descobrir a aceleração angular do rodízio. De acordo com a figura abaixo, onde o ponto D é um ponto de contato do rodízio com o solo:

a → A = a → D + a A / D

a A i → = a D x i → + a D y j → + α A k → × - r A D j → - ω A 2 - r A B j → = a D x i → + a D y j → + ( α A r A D ) i → - ω A 2 - r A B j →

a A = α A r A D →   2,4 = α A ⋅ 0,025

α A = 96   r a d / s 2

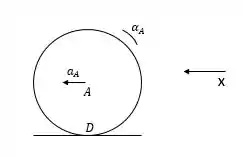
Passo 2

Para descobrir a aceleração angular do cilindro, vamos fazer de modo semelhante ao passo 1:

a → E = a E x i → + a E y j → = a C i → = 2,4 i →

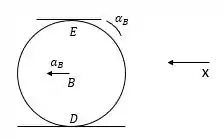
A aceleração do ponto E será igual a aceleração do carrinho, pois esse é o ponto de contato ente o cilindro e o carrinho. Assim, podemos relacionar o ponto E e o ponto D:

a → E = a → D + a → E / D → 2,4 i → = 0 + α B k → × - r E D j → - ω B 2 - r E D j → = α B r E D i → + ω B 2 r E D j →

2,4 = 0,050 α B → α B = 48   r a d / s 2

Passo 3

Com esses dados, podemos calcular a aceleração do ponto B:

a B = r B D α B

a B =   0,025 ⋅ 48 = 1,2   m / s 2

Resposta

  1. 96 rad/s²; 48 rad/s²
  2. 2,4 m/s²; 1,2 m/s²
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No dado instante, o membro AB tem o movimento angular mostrado. Determine a velocidade e a aceleração do bloco deslizante C nesse instante.
O cilindro hidráulico se estende com uma velocidade v A = 1,5m / s e uma aceleração a A = 0,5m / s 2 . Determine a aceleração angular do membro ABC e a aceleração da extremidade C no instante mostrado
O cilindro hidráulico D se estende com a velocidade v B = 1,2m / s e uma aceleração a B = 0,45m / s 2 . Determine a aceleração de A no instante mostrado.
O cilindro hidráulico D se estende com uma velocidade v B = 1,2m / s e uma aceleração a B = 0,45m / s 2 . Determine a aceleração de C no instante mostrado.
O bloco deslizante se desloca com uma velocidade v B = 1,5m / s e uma aceleração a B = 0,9m / s 2 . Determine a aceleração angular da barra AB no instante mostrado.