Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 149

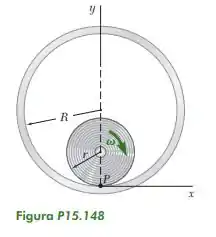
15.149. No Problema 15.148, mostre que a trajetória de P é uma linha reta vertical quando r= R /2. Deduza expressões para a velocidade e aceleração de P correspondentes em qualquer instante t.

Passo 1

Vamos começar o problema definindo dois ângulos, θ e ϕ .

θ indica o movimento do ponto P em torno do círculo menor e ϕ indica a o movimento do circulo menor em torno do círculo maior.

Passo 2

A gente pode assumir que

d θ d t = ω

E

θ = ω t

A roda gira sem deslizar, então podemos concluir que o arco OC é igual ao arco PC.

Temos

P C = r θ + ϕ

E

O C = R ϕ

Sendo r o raio da roda interna e R o raio da roda externa.

Então

r θ + ϕ = R ϕ

Mas o enunciado nos diz que

r = R 2

Ou

R = 2 r

Então

r θ + ϕ = 2 r ϕ

Isso fica

r θ + r ϕ = 2 r ϕ

θ = ϕ

Passo 3

Agora podemos assumir que

x = R - r sin ⁡ ϕ - r sin ⁡ θ

x = 2 r - r sin ⁡ θ - r sin ⁡ θ

Então

x = r sin ⁡ θ - r sin ⁡ θ = 0

E

y = R - R - r cos ⁡ ϕ - r cos ⁡ θ

y = R - 2 r - r cos ⁡ θ - r c o s   θ

Então

y = 2 r - 2 r c o s   θ  

y = 2 r 1 - cos ⁡ θ

Vamos derivar

x ˙ = 0

Então no eixo x a posição não varia, logo o movimento é uma linha vertical.

E

y ˙ = v y = 2 r θ ˙ sin ⁡ θ

Ou então

v y = R ω sin ⁡ ω t

Agora vamos fazer

a = v ˙

a x = 0

a y = d d t 2 r θ ˙ sin ⁡ θ

Essa derivada fica

a y = 2 r   θ ˙ 2 cos ⁡ θ - θ ¨ sin ⁡ θ

Isso fica

a y = R ω 2 cos ⁡ θ - α sin ⁡ θ

Mas no exercício anterior, o enunciado diz que ω é constante, logo a aceleração angular é nula, por tanto

a y = R ω 2 cos ⁡ θ

Resposta

v = 0   i ^ +   R ω sin ⁡ ω t   j ^

a = 0   i ^ + R ω 2 cos ⁡ θ   j ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tambor de 100 mm de raio está preso rigidamente a um cilindro de 180 mm de raio. Uma corda é enrolada ao redor do tambor e sua extremidade E é puxada para a direita com velocidade constante de 400
Resolva o Problema 15.166 admitindo que a direção da velocidade relativa u seja invertida, de modo que a porção B D esteja sendo retraída.
A barra A B de comprimento R gira em torno A com velocidade angular constante ω 1 no sentido horário. Ao mesmo tempo, a barra B D de comprimento r gira em torno de B com velocidade angular constante ω
A barra A B de comprimento R = 300m m gira em torno A com velocidade angular constante ω 1 de 5r a d / s no sentido horário. Ao mesmo tempo, a barra B D de comprimento r = 160m m gira em torno de B co
O volante com raio de 18 pol. Está rigidamente preso a um volante de 1,5 pol. - eixo de raio que pode rolar ao longo de trilhos paralelos. Sabendo que no instante mostrado o centro do eixo tem uma vel