Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 46
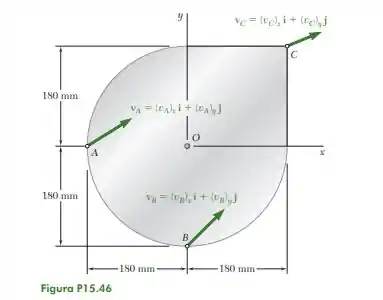
15.46. A placa mostrada na figura desloca-se no plano xy. Sabendo que (vA)x 120 mm/s, (vB)y 300 mm/s e (vC)y 60 mm/s, determine (a) a velocidade angular da placa, (b) a velocidade do ponto A.
Passo 1
Vamos matar mais uma?
Antes de começar a resolver o exercício a gente já é capaz de dizer uma coisa, a velocidade angular tem uma única componente em .
Isso porque a placa se move exclusivamente no plano , então a velocidade angular tem que ser perpendicular a esse plano.
Vamos começar destacando as informações importantes:
Essas informações vão ser úteis para a gente, porque podemos fazer o seguinte:
Sendo que é a velocidade relativa entre e . A velocidade relativa é calculada assim:
Passo 2
Então temos
E isso fica
E nós conhecemos esses vetores:
Então
Se nós resolvermos para a componente vamos ficar com:
Então
Passo 3
Agora vamos para o item (b). Vamos determinar a velocidade do ponto A. Vamos usar um raciocínio similar ao que fizemos no item anterior.
E sabemos que
Então
Vamos lá, sabemos que
Vamos substituir os valores:
Isso fica
Se a gente resolver para a componente em
Então