Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 71
71. Se o cilindro hidráulico encurta-se a uma taxa constante de , determine a velocidade da extremidade A da barra de ligação ACB no instante mostrado.
Passo 1
Um esboço que pode ajudar na resolução do problema pode ser representado por:
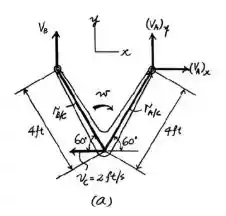
Passo 2
Aplicando a equação da velocidade relativa na figura a, teremos que:
Igualando a componente:
Resolvendo,
Passo 3
Relacionando o ponto A e C utilizando o resultado acima:
Igualando as equações, podemos obter:
Então,
Resposta
Exercícios de Livros Relacionados
Um pêndulo composto é definido como uma placa rígida que oscila em torno de um Ponto O fixo denominado centro de suspensão. Mostre que o período de oscilação de um pêndulo composto é igual ao período
A barra uniforme AB de 8 kg é articulada em C e está ligada em A a uma mola de constante k = 500 Wm. Se a extremidade A receber um pequeno deslocamento e for liberada, determine (a) a frequência das p
Uma haste delgada de 6 libras é suspensa de um fio de aço que é conhecido por ter uma torção. constante da mola K = 1,5 ft . lb / rad. Se a haste for girada 180 ° em torno da vertical e liberada, dete
A haste ABC de massa total em é dobrada como mostrado e é suportada em um plano vertical por um pino em B e por uma mola de k constante em C. se a extremidade C receber um pequeno deslocamento e for l
Um disco uniforme de raio r = 250 mm é fixado em A a uma haste AB de 650 mm de massa desprezível que pode girar livremente em um plano vertical em torno de B. se a haste for deslocada 2 ° da posição m