Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 30
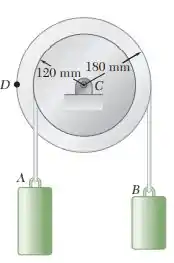
Uma polia e dois blocos estão conectados por cabos inextensíveis como mostra a figura. O bloco tem uma aceleração constante de e uma velocidade inicial de , ambas direcionadas para baixo. Determine o número de revoluções executadas pela polia em , a velocidade e posição do bloco B após , a aceleração do ponto na borda da polia em .
Passo 1
Fala, galera. Beleza? Bora para mais um exercício de Dinâmica. Vamos dividir este exercício em três partes. Na primeira, temos que encontrar o número de revoluções executadas pela polia em .
Sabemos que os cabos são inextensíveis, logo, a velocidade inicial no ponto é igual à velocidade inicial no ponto , localizado na tangência da polia com a corda que prende o corpo :
Assim como a velocidade, a aceleração nestes dois pontos também será igual:
Com isso, a partir da distância dos pontos tangentes até o centro da polia, podemos escrever:
E também:
Assim, vamos utilizar as equações do movimento uniformemente acelerado para a fim de obtermos o número de revoluções. Sabemos que a velocidade angular é dada por:
Substituindo:
E para a variação angular, temos:
Agora que sabemos a distância angular percorrida, vamos utilizar este valor para determinar o número de revoluções. Como revolução representa uma distância percorrida de , podemos encontrar o número de revoluções assim:
Passo 2
Na próxima parte do exercício, temos que determinar a velocidade e a posição do bloco após . Bora lá!
Podemos utilizar a relação entre o raio da polia para o carregamento e o momento linear. Com isso, podemos determinar a velocidade do bloco. Fica assim:
E para a variação da posição do bloco, vamos relacionar o mesmo raio com o momento angular. Logo:
Opa, galera. Agora que encontramos a velocidade a o deslocamento, só falta mais um passo.
Passo 3
Na última parte do nosso problema, temos que determinar a aceleração do ponto na borda da polia em Para isso, vamos novamente relacionar o raio com a aceleração angular, porém, queremos inicial. Logo:
E também:
Opa, temos dois vetores aceleração e a soma deles, vai ser a aceleração em . Assim:
É isso, galerinha. Bora praticar mais!