Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 156
156. Substitua o carregamento por uma força resultante e momento de binário equivalentes que agem no ponto .
Passo 1
Vamos resolver esse problema separando em duas partes, a primeira parte é o carregamento inclinado a esquerda e a segunda é o carregamento mais acima que está na horizontal.
A intensidade da força é igual a área total sob o diagrama de carregamento, isso vale para as duas partes que temos na figura.
A posição do centroide em relação ao próprio diagrama, que é onde essa força atua é dada pela seguinte fórmula:
Mas para figuras geométricas mais simples, como o nosso caso, tem fórmulas tabeladas que você pode encontrar no apêndice C na seção C.4.
O carregamento que está inclinado pode ser divido em duas figuras que tem forma fácil de calcular a área, nesse caso vai ser um triângulo e um retângulo como é mostrado a seguir na figura:
Achando as forças que representam cada carregamento, vamos decompô-las em suas componentes verticais e horizontais, acharemos a resultante em cada direção podendo montar a força resultante total como um vetor, depois para achar sua intensidade basta calcular a norma desse vetor.
Para achar o momento de binário, basta somar o momento referente de cada força e somá-los.
Passo 2
Agora vamos calcular as forças do carregamento inclinado. Como a força é igual a área do diagrama, vamos chamar de a força referente ao retângulo e a força referente ao triângulo, então:
Agora vamos calcular onde essas forças atuam.
Passo 3
Agora vamos calcular do carregamento superior. Vamos chamar de a força que representa esse carregamento e dada por:
Agora vamos calcular onde essa força atuam.
Passo 4
Agora observando a figura abaixo, podemos ver a seguinte semelhança de ângulos, que vai nos ajudar a decompor as forças e .
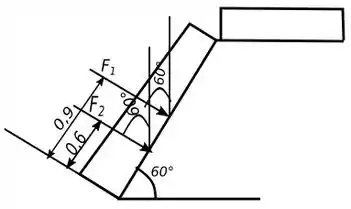
Com isso, podemos decompor e , da seguinte maneira:
Vertical:
Horizontal:
Passo 5
Agora vamos calcular as componentes da força resultante na vertical e na horizontal.
Vertical:
Horizontal:
Logo:
A direção dessa força é determinada por:
Passo 6
Vamos agora determinar o momento de binário, para isso basta somar o momento de cada força, que nada mais é que a força multiplicada pela a distância de sua aplicação até o ponto que queremos que no caso vai ser o , para achar essa distância, vamos ver a figura abaixo que nos mostra o que temos até agora:
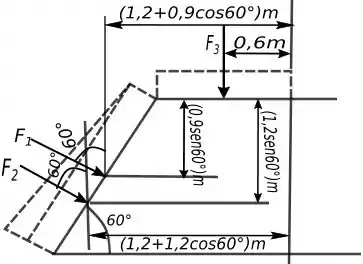
Essas distâncias são encontradas analisando o quanto você deve andar para cada direção do ponto até cada uma das forças.
Com isso, tanto as componentes verticais quanto as componentes horizontais das forças, vão desempenhar um papel no cálculo do momento.
Então: