Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 2
Determine o par M necessário para manter o equilíbrio em um ângulo . Cada uma das duas barras uniformes tem massa m e tem comprimento l.
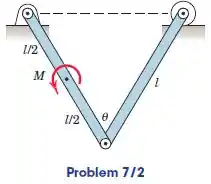
Fonte: Meriam - Estática - 7ª ed
Passo 1
Olá meus amores!
Vamos pegar esse embalo!
Bem, iniciamos o capítulo com esse problema que fala em equilíbrio, mais precisamente pede o ângulo para que o sistema permaneça em equilíbrio.
Vamos lá relembrar como devemos pensar quando há problemas pedindo algo quando o sistema está em equilíbrio:
No entanto, apresentamos o conceito de trabalho virtual para uma partícula para que possamos posteriormente aplicar para sistemas de partículas, que é a seguinte:
Passo 2
Com os conceitos refrescados e o diagrama de corpo livre podemos inserir no problema:
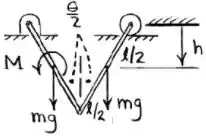
Assim, podemos inferir primeiro que o deslocamento virtual das barras se dá no eixo y, devido a não informação sobre alguma força atuante no eixo x:
E derivando, temos:
Passo 3
Como o sistema pede o equilíbrio, podemos as forças e momentos que interferem no deslocamento virtual são o momento M dado no problema e os pesos das barras. Assim:
Substituindo valores, temos:
Assim:
Resposta
Portanto