Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 1
A massa da barra uniforme de comprimento l é m enquanto a da barra uniforme de comprimento 2l é 2m. Para uma dada força P, determine o ângulo de equilíbrio.
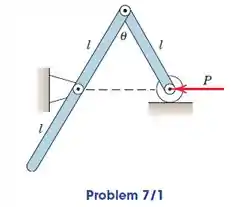
Fonte: Meriam - Estática - 7ª ed
Passo 1
Olá meus amores!
Bora iniciar esse capítulo top que fala de trabalho virtual!
Bem, iniciamos o capítulo com esse problema que fala em equilíbrio, mais precisamente pede o ângulo para que o sistema permaneça em equilíbrio.
Vamos lá relembrar como devemos pensar quando há problemas pedindo algo quando o sistema está em equilíbrio:
No entanto, apresentamos o conceito de trabalho virtual para uma partícula para que possamos posteriormente aplicar para sistemas de partículas, que é a seguinte:
E relembremos o princípio do trabalho virtual:
“O trabalho virtual realizado por forças ativas externas em um ideal sistema mecânico em equilíbrio é zero para todo e qualquer deslocamentos virtuais consistentes com as restrições.”
Passo 2
Vejamos o diagrama do corpo livre do problema:
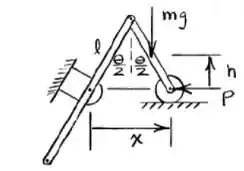
Assim, podemos inferir primeiro que (em x), o deslocamento virtual se dá:
Derivando a equação:
E da mesma forma em y, o deslocamento virtual é:
E
Passo 3
Como o sistema pede o equilíbrio, podemos inferir que
Assim:
Substituindo valores, temos:
Assim:
Resposta
Portanto