Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 18
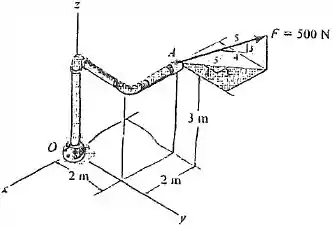
18. Determine o momento da força em relação aos eixos x, y e z. Use uma análise escalar.
Passo 1
Fala, querido! Queremos o momento de em relação aos 3 eixos coordenados. Mas ele pede para usar uma abordagem escalar.
Para resolver esse exercício vamos usar o método de análise escalar que é baseada na fórmula:
Onde d nesse caso é menor distância entre o eixo em relação ao qual queremos o momento e a linha de ação da força. Lembra, se é distância, esse segmento de comprimento faz com a linha de ação da força.
Nessa situação teremos que decompor nossas forças em relação aos eixos coordenados.
Assim temos três componentes que importam que são , e .
Vamos definir também o sentido positivo do momento conforme a regra da mão direita.
Bora!
Passo 2
Agora vamos descobrir as componentes da nossa força.
Se você reparar, na nossa figura temos dois pequenos triângulos, mas para que estão lá? Eles indicam que há uma relação de proporcionalidade entre os lados do triângulo e as componentes da força paralelas a cada lado.
Vamos olhar para o triângulo em pé.
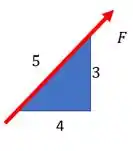
O lado 3 é paralelo ao eixo , então para descobrir a força em a gente pode usar a semelhança de triângulos, imaginando que a força é um lado de um triângulo proporcional ao azul:
Precisamos descobrir a projeção dessa força em , para achar as outras componentes. Esse plano é paralelo ao lado 4 do triângulo.
Aí a gente acha as componentes em e através de e do triângulo deitado:
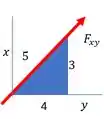
O eixo é paralelo ao lado que tem valor 3:
E o eixo é paralelo ao lado de valor 4:
Então:
Passo 3
Agora vamos calcular o momento referente a cada eixo que foi pedido, começaremos com o eixo x.
Temos que para o eixo de rotação, sendo o eixo x, a força na direção x não colabora para o momento ou produz qualquer tendência para girar já que ela é paralela ao eixo de rotação.
Vamos pensar sobre os valores de para as forças que sobraram. precisa ser a distância entre e a linha de ação de . Pela figura, isso vai ser numericamente a coordenada do ponto , então
E para , queremos a distância entre o eixo e linha de ação da força . Se a gente prolongar a linha de ação da força e o eixo , vemos que ela é a coordenada de :
Assim nosso momento em relação ao eixo de rotação x é:
A primeira componente é negativa pois faz com que o objeto rode no sentido horário em relação ao eixo x.
Continuando:
Passo 4
Vamos calcular o momento em relação ao eixo de rotação y.
Temos que para o eixo de rotação, sendo o eixo y, a força na direção y não colabora para o momento ou produz qualquer tendência para girar já que ela é paralela ao eixo de rotação.
Para achar aqui fazemos o mesmo raciocínio. A distância de até a linha da força é 3, a coordenada de :
Fazendo a mesma análise para :
Assim nosso momento em relação ao eixo de rotação y é:
A primeira componente é negativa pois faz com que o objeto rode no sentido horário em relação ao eixo y.
Continuando:
Passo 5
Agora calculando o momento em relação ao eixo de rotação z.
Temos que para o eixo de rotação, sendo o eixo z, a força na direção z não colabora para o momento ou produz qualquer tendência para girar já que ela é paralela ao eixo de rotação.
Aí fazemos as análises para achar :
Assim nosso momento em relação ao eixo de rotação z é:
A primeira componente é negativa pois faz com que o objeto rode no sentido horário em relação ao eixo z.
Continuando:
Resposta
Momento em relação ao eixo x:
Momento em relação ao eixo y:
Momento em relação ao eixo z: