Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 1

  1. Determine, em função do ângulo θ , o momento M , aplicado através do eixo a conexão inferior, necessário para suportar a carga P . Despreze os pesos das partes.

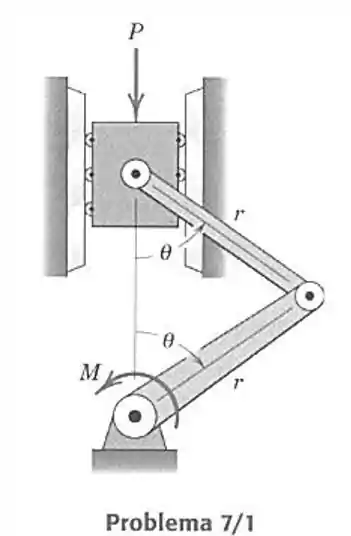
Passo 1

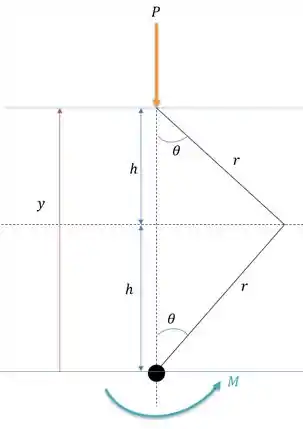
Vamos traçar nossas linhas de deslocamento virtual no sistema :

A fórmula da teoria de trabalhos virtuais nos diz que:

δ U = 0

Onde U é o trabalho existente no sistema todo.

Onde a força P tende a diminuir a tamanho da distância perpendicular a ela que nos caso é a distância y toda, logo:

δ U p = - P δ y

E o momento M tende a diminuir o ângulo θ intrínseco a ela, logo:

δ U M = - M δ θ

Como U é o trabalho no sistema todo logo:

U = U M + U θ

δ U = - P δ y - M δ θ = 0

Passo 2

Agora precisamos encontrar alguma relação entre θ e y para que possamos definir melhor o que é de fato o momento M , pois note que é para isso que desenhamos a distância h , pois conseguimos tirar alguma relação com essa variável intermediária (já que os dois braços formam um triângulo isósceles).

y = 2 h

cos ⁡ θ = h r → h = r cos ⁡ θ

y = 2 r c o s   θ

Logo a equação de trabalho virtual do sistema fica:

- P δ ( 2 r cos ⁡ θ ) = M δ θ

- 2 Pr ⁡ ( - sin ⁡ θ   δ θ ) = M   δ θ

Não se esquecendo da regra da cadeia onde devemos derivar θ e cortando δ θ .

2 Pr ⁡ sin ⁡ θ = M

Resposta

M = 2 Pr ⁡ sin ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra uniforme A B tem um peso de 50 N . Se a mola D C está livre quando θ = 0 ° , determine o ângulo θ para o equilíbrio usando o princípio do trabalho virtual. A mola sempre permanece na posição h
As ligações uniformes A B e B C pesam cada uma 10 N e o cilindro pesa 100 N . Determine a força horizontal P necessária para manter o mecanismo em θ = 45 ° . A mola tem um comprimento livre de 150 m m
O virabrequim está sujeito a um torque M = 75 N ⋅ m . Determine a força compressiva vertical F aplicada ao pistão para o equilíbrio quando θ = 60 ° .
Determine o peso do bloco G necessário para equilibrar a balança diferencial quando a carga F de 100N( ≈ 10k g ) é colocada na panela. A balança está em equilíbrio quando a carga e o bloco não estão n
Se a carga F pesa 100N e o bloco G pesa 10N , determine sua posição x para o equilíbrio da balança diferencial. A balança está em equilíbrio quando a carga e o bloco não estão na balança.