Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 41
2.41. Determine a intensidade e a direção θ de , de modo que a força resultante seja direcionada ao longo do eixo y positivo e tenha uma intensidade de .
Passo 1
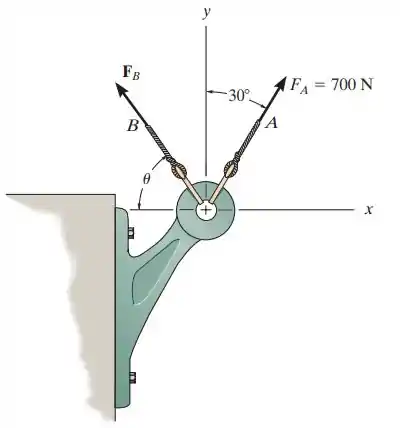
Fala ai galerinha bonita, tudo belezinha?! Se liga só, esse exercício aqui disse pra gente que temos duas forças e atuando sobre um suporte mais ou menos como na figura abaixo:
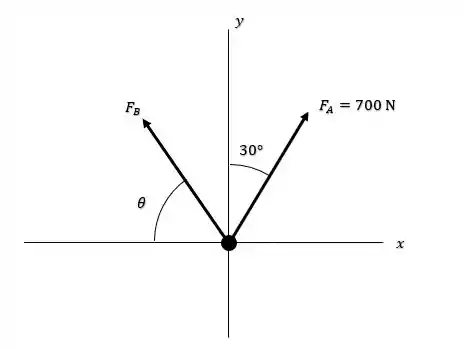
E sabendo disso ele pede pra gente encontrar o valor de e de modo que a força resultante de a esteja na mesma direção do eixo positivo e com intensidade de .
Show de bolinhas, quando ele diz que a força resultante vai estar na direção positiva do eixo , quer dizer que pela regra do paralelogramo a soma de e vai estar nessa direção, tal que:
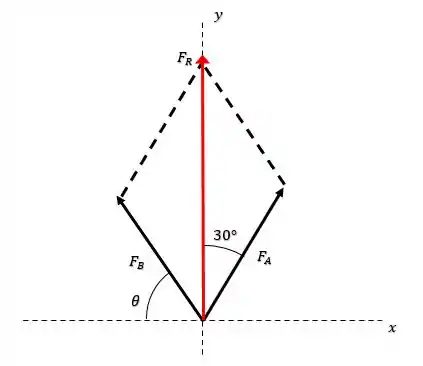
Onde é a força resultante.
Passo 2
Mas a malandragem aqui é que como a resultante está somente no eixo , quer dizer que as forças se anulam no eixo , logo:
E como a soma no eixo equivale a , então teremos que:
Se a gente isolar na primeira equação, vamos obter que:
Substituindo esse resultado na outra equação:
Como , podemos organizar os termos como:
Logo, substituindo valor de , de e de , obtemos que:
Isolando :
Sendo assim, o valor de será:
Passo 3
Agora que a gente já descobriu o ângulo, ficou xuxu beleza encontrar o valor de , como vimos que:
Substituindo os valores que conhecemos, vamos descobrir que:
