Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 56

18.56. Determine a taxa de variação G da quantidade de movimento angular HG do disco do Problema 18.2.

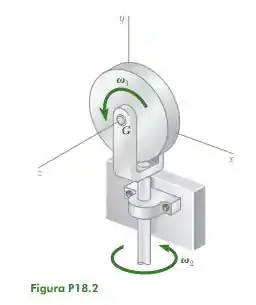
Passo 1

Vamos começar relembrando o problema 18.2. No problema temos um disco fino de massa m e raio r com uma velocidade angular ω 1 . Esse disco está apoiado em uma união U presa numa barra vertical que gira com uma velocidade angular ω 2 .

A velocidade angular do sistema vai ser

ω = ω 2   j ^ + ω 1   k ^

Passo 2

Vamos calcular os momentos de inercia.

I x = 1 4 m r 2 + 1 12 m L 2

Sendo L a espessura do disco, mas para esse problema podemos desprezar essa espessura, então

I x = 1 4 m r 2

Analogamente

I y = 1 4 m r 2

E por último

I z = 1 2 m r 2

Passo 3

Agora a gente tem tudo para calcular o momento angular:

H G = I x ω x   i ^ + I y ω y   j ^ + I z ω z   k ^

Substituindo os valores

H G = 1 4 m r 2 ( 0 )   i ^ + 1 4 m r 2 ω 2   j ^ + 1 2 m r 2 ω 1   k ^

Então

H G = 1 4 m r 2 ω 2   j ^ + 1 2 m r 2 ω 1   k ^

As coisas vão facilitar agora por que ω está girando em torno do ponto G, então podemos assumir

ω = Ω

Agora vamos calcular a taxa de variação

H ˙ G = Ω × H G

Isso fica

H ˙ G = ω 2   j ^ + ω 1   k ^ × 1 4 m r 2 ω 2   j ^ + 1 2 m r 2 ω 1   k ^

Fazendo esse produto vetorial, vamos ficar com

H ˙ G = 1 2 m r 2 ω 1 ω 2   i ^

Resposta

H ˙ G = 1 2 m r 2 ω 1 ω 2   i ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa triangular e duas placas retangulares estão soldadas entre si e à barra reta A B . A unidade soldada gira como um todo em torno do eixo A B com uma velocidade angular constante de 5r a d/ s
No Problema 15.10, determine a velocidade e a aceleração do canto H admitindo que a velocidade angular é de 9r a d / s e decresce a uma taxa de 18r a d/ s 2 .
Resolva o problema 15.3 para t = 1 s .
Uma placa circular mostrada na figura está inicialmente em repouso. Sabendo que r = 200m m e que a placa tem uma aceleração angular constante de 0,3r a d / s 2 , determine a intensidade da aceleração
A barra dobrada A B C D E gira em torno de uma linha que liga os pontos A e E com uma velocidade angular constante de 9r a d / s . Sabendo que a rotação é horária a partir de E , determine a velocidad