Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 27

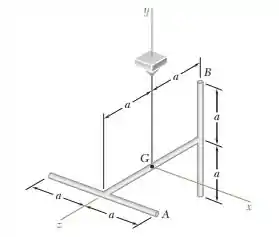
Três barras esbeltas, cada uma com massa m e comprimento 2a, são soldadas para formar a estrutura mostrada na figura. A estrutura é atingida em A em uma direção vertical descendente. Representando o impulso correspondente por F → Δ t , determine, imediatamente após o impacto, (a) a velocidade do centro de massa G, (b) a velocidade angular da barra.

Passo 1

Vamos resolver mais essa. Vamos definir primeiramente os momentos e os produtos de inércia relacionado as barras. A barra 1 tem o ponto B, a barra 2 tem o ponto G e a barra 3 tem o ponto A. Logo,

I - x = I x 1 + I x 2 + I x 3 = m a 2 + 1 3 m a 2 + m a 2 + a 2 3 = 8 3 m a 2

I - y = I y 1 + I y 2 + I y 3 = m a 2 + a 2 3 + 1 3 m a 2 + m a 2 = 8 3 m a 2

I - z = I z 1 + I z 2 + I z 3 = 1 3 m a 2 + 0 + 1 3 m a 2 = 2 3 m a 2

I - x y = 0 ,   I - y z = 0 , I - z x = 0

Passo 2

Vamos calcular a velocidade do centro de massa utilizando o princípio de impulso e quantidade de movimento. Os impulsos consistem da força aplicada no sentido para baixo em A, - F Δ t j → , e da força de tração aplicada em G, T Δ t j → . Por causa do fio estar conectado em G, v y = 0 . Assim,

T Δ t j → - F Δ t j → = m v → x i → + m v → z k →

Assim,

T Δ t = F Δ t

v x = 0 ,   v z = 0

v → = 0

Passo 3

Agora vamos calcular a velocidade angular da barra. Igualando os momentos angulares em G:

a i → + a k → × - F Δ t j → = H x i → + H y j → + H z k →

a F Δ t i → - a F Δ t k → =   H x i → + H y j → + H z k →  

H x = a F Δ t → I - x ω x = a F Δ t → 8 3 m a 2 ω x = a F Δ t

ω x = 3 F Δ t 8 m a

H y = 0 → ω y = 0

H z = - a F Δ t → I - z ω z = a F Δ t → 2 3 m a 2 ω x = - a F Δ t

ω x = - 3 F Δ t 2 m a

Logo,

ω → = 3 F Δ t 8 m a i → - 4 k →

Resposta

  1. v → = 0
  2. ω → = 3 F Δ t 8 m a i → - 4 k →
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois discos de atrito A e B , ambos rodando livremente a 240r p m no sentido anti-horário, são postos em contato. Após 8s de deslizamento, durante o qual cada disco tem uma aceleração angular constant
Um dispositivo simples de acionamento por atrito consiste em dois discos, A e B . Inicialmente, o disco A tem uma velocidade angular de 500r p m e o disco B encontra-se em repouso. Sabe-se que o disco
O anel B tem um raio interno r 2 e está suspenso por um eixo horizontal A do modo mostrado na figura. O eixo A gira com velocidade angular constante de 25r a d/ s e não ocorre deslizamento. Sabendo qu
O anel B tem um raio interno r 2 e está suspenso por um eixo horizontal A do modo mostrado na figura. Sabendo que o eixo A gira com velocidade angular constante w A e que não ocorre deslizamento, dedu
Em um processo contínuo de impressão, o papel é puxado para dentro das prensas a uma velocidade constante v . Representando por r o raio do rolo de papel em um instante dado qualquer e por b a espessu