Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 66

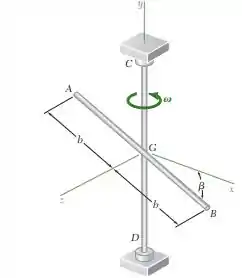
18.66. Uma barra AB uniforme e delgada de massa m e um eixo vertical CD, cada com comprimento 2b, são soldados juntos em seus pontos médios G. Sabendo que o eixo gira numa taxa constante, determine as reações dinâmicas de C e D.

Passo 1

Vamos lá, esse problema aqui vai exigir que a gente use s eixos principais G x ' y ' z ' , que estão na figura:

Em que

z ' = z

E também é importante notar que

ω → = ω   j ^

Passo 2

Vamos calcular os momentos de inércia nos eixos G x ' y ' z ' .

I x ' = 0

E

I y ' = I z ' = 1 3 m b 2

Pela imagem também podemos deduzir

ω x ' = - ω sin ⁡ β  

ω y ' = ω cos ⁡ β

E

ω z ' = 0

Passo 3

Agora temos tudo para calcular o momento angular no ponto G.

H → G = I x ' ω x '   i ^ ' + I y ' ω y '   j ^ ' + I z ' ω z '   k ^ '

Isso aqui fica

H → G = 0 - ω sin ⁡ β     i ^ ' + 1 3 m b 2 ω cos ⁡ β   j ^ ' + 1 3 m b 2 0   k ^ '

Então

H → G = 1 3 m b 2 ω cos ⁡ β   j ^ '

Mas olha só, j ^ ' está na direção de y ' , então se olharmos de novo a imagem

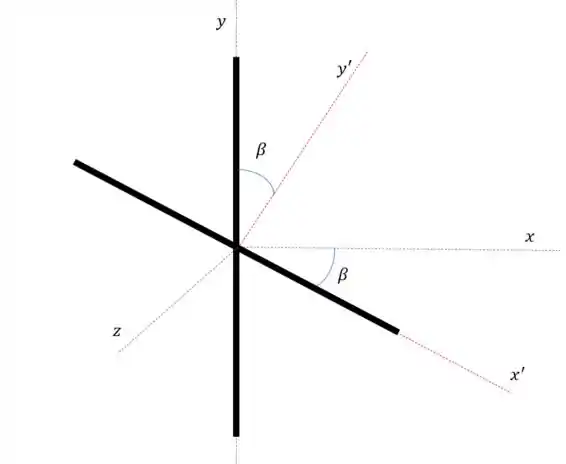
A gente percebe que

j ^ ' = sin ⁡ β   i ^ + cos ⁡ β   j ^

Então para colocar H → G nos eixos cartesianos só precisamos fazer:

H → G = 1 3 m b 2 ω cos ⁡ β   sin ⁡ β   i ^ + cos ⁡ β   j ^

Ou então

H → G = 1 3 m b 2 ω cos ⁡ β sin ⁡ β i ^ + 1 3 m b 2 ω cos 2 ⁡ β j ^

Passo 4

Agora vai dar uma facilitada para a gente, porque ω é constante, isso significa que

H → ˙ G G x y z = 0

E como estamos no nosso referencial rotacional, podemos assumir

Ω → = ω →

Então

H → ˙ G = H → ˙ G G x y z + Ω → × H → G

Pode ser simplificado para

H → ˙   G = ω → × H → G

Agora vamos calcular

H → ˙ G = ω   j ^ × 1 3 m b 2 ω cos ⁡ β sin ⁡ β i ^ + 1 3 m b 2 ω cos 2 ⁡ β j ^

Isso vai ficar

H → ˙ G = - 1 3 m b 2 ω 2 cos ⁡ β sin ⁡ β   k ^

Passo 5

Agora nós podemos fazer

∑ M → D = H → ˙ G

Já que as forças que de fato são efetivas no ponto D podem ser calculadas com H → ˙ G .

Beleza, vamos quais as forças estão no sistema.

Então:

∑ M → D = 2 b   j ^ × C x   i ^ + 2 b   j ^ × C z   k ^

Isso fica

∑ M → D = - 2 b C x   k ^ + 2 b C z   i ^

Agora podemos substituir os valores na equação

∑ M → D = H → ˙ G

- 2 b C x   k ^ + 2 b C z   i ^ = - 1 3 m b 2 ω 2 cos ⁡ β sin ⁡ β   k ^

Agora tudo que falta para descobrirmos C → é igualar a equação por coeficiente. No coeficiente i ^ temos:

2 b C z = 0

Isso implica

C z = 0

E no coeficiente k ^ :

- 2 b C x = - 1 3 m b 2 ω 2 cos ⁡ β sin ⁡ β

Isso implica

C x = 1 6 m b ω 2 cos ⁡ β sin ⁡ β

Então

C → = 1 6 m b ω 2 cos ⁡ β sin ⁡ β   i ^ N

Bom, para esse sistema podemos dizer que

C → + D → = 0

Então

D → = - C → = - 1 6 m b ω 2 cos ⁡ β sin ⁡ β   i ^ N

E assim terminamos o problema.

Resposta

C → = 1 6 m b ω 2 cos ⁡ β sin ⁡ β   i ^ N

D → = - 1 6 m b ω 2 cos ⁡ β sin ⁡ β   i ^ N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A polia dupla mostrada na figura tem massa de 15 kg e um raio de giração centroidal de 160 mm. O cilindro A e o bloco B estão presos a cordas enroladas sobre as polias, conforme ilustrado na figura. O
Dois discos de mesmo material estão presos a um eixo como mostrado na figura. O disco A tem massa de 15 kg e um raio r = 125mm. O disco B tem o triplo da espessura do disco A. Sabendo que um binário M
Cada uma das engrenagens A e B tem uma massa de 2,4 kg e um raio de giração de 60 mm, enquanto a engrenagem C tem uma massa de 12 kg e um raio de giração de 150 mm. Um binário M de intensidade 10 N ∙
Resolva o Problema, considerando que a binário 10 N ∙ m é aplicado na engrenagem B.
Os três discos de atrito mostrados na figura são feitos do mesmo material e tem a mesma espessura. Sabe-se que o disco A tem massa de 6 kg e que os raios dos discos são rA = 200 mm, rB = 150 mm e rC =