Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 4

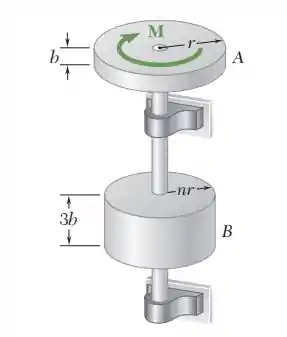
Dois discos de mesmo material estão presos a um eixo como mostrado na figura. O disco A tem massa de 15 kg e um raio r = 125mm. O disco B tem o triplo da espessura do disco A. Sabendo que um binário M de intensidade 20 N ∙ m é aplicado ao disco A quando o sistema está em repouso, determine o raio n r do disco B para que a velocidade angular do sistema seja de 600 rpm após quatro revoluções.

Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente determine o raio n r do disco B para que a velocidade angular do sistema seja de 600 rpm após quatro revoluções.

Para qualquer disco: m = ρ π r 2 t

Ī = 1 2   m r 2 = 1 2   π ρ t r 4

Passo 2

Momento de Inércia:

Disco A: I A = 1 2   π ρ b r 4

Disco B: I B = 1 2   π ρ ( 3 b ) ( n r ) 4 = 3 n 4 1 2   π ρ b r 4 = 3 n 4   I A

I t o t a l = I A   + I B = 1 + 3 n 4   I A

Passo 3

Velocidade angular: ω 1 = 0

ω 2 = 600   r p m = 20   π   r a d / s

Rotação: θ = 4   r e d = 8   π   r a d

Energia Cinética: T 1 = 0

T 2 =   1 2   I t o t a l     ω 2 2

Passo 4

Trabalho: U 1 → 2 = M θ = ( 20   N ∙ m ) ( 8   π   r a d ) = 502.65   J

Princípio do trabalho e energia: T 1 + U 1 → 2 = T 2

0 + 502.65 = 1 2 I t o t a l 20   π 2

I t o t a l = 0.25465   K g ∙ m 2

I A = 1 2   m A   r A 2 = 1 2 15   K g 0.125   m 2 = 0.117188   K g ∙ m 2

A partir de: 0.25465 = 1 + 3 n 4 0.117188

n 4 = 0.390998

n = 0.79076

Raio do disco B: r B = n r A = ( 0.79076 ) ( 125   m m )

Resposta

r B = 98.8   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a Terra fosse uma esfera, a atração gravitacional do Sol, da Lua e dos planetas seria sempre equivalente a uma única força R agindo no centro de massa da Terra. No entanto, a Terra é na verdade um
Referindo-se ao Problema 18.143, (a) provar que o elipsóide de Poinsot é tangente ao plano invariável, (b) mostrar que o movimento do corpo rígido deve ser tal que o elipsóide de Poinsot pareça rolar
O topo de 85 g mostrado é suportado no Ponto fixo 0. Os raios de giração do topo em relação ao seu eixo de simetria e em relação a um eixo transversal em 0 são 21 mm e 45 mm, respectivamente. Sabendo
O topo mostrado é suportado no Ponto fixo 0 e seus momentos de inércia em torno de seu eixo de simetria e em torno de um eixo transversal em 0 são denotados, respectivamente, por I e I ' . (a) Mostre
Uma esfera sólida de raio c = 3 pol. É anexada como mostrado ao cabo AB. Observa-se que a esfera processa a uma taxa constante ϕ ˙ = 6 r a d / s em torno do eixo vertical AD. Sabendo que β = 40 ∘ , de