Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 15

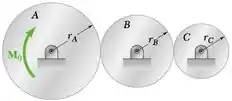
Os três discos de atrito mostrados na figura são feitos do mesmo material e tem a mesma espessura. Sabe-se que o disco A tem massa de 6 kg e que os raios dos discos são rA = 200 mm, rB = 150 mm e rC = 100 mm. O sistema está em repouso quando um binário M0 de intensidade constante 7,5 N ∙ m é aplicado no disco A. Considerando que não ocorre nenhum escorregamento entre os discos, determine o número de revoluções requerido para o disco A para alcançar a velocidade angular de 150 rpm.

Passo 1

O exercício pede que a gente determine o número de revoluções requerido para o disco A para alcançar a velocidade angular de 150 rpm.

A massa de um disco é dada por:

m = volume ρ = π r 2 t p

E a inércia por:

I - = 1 2 m r 2 = π ρ t 2 r 4

Passo 2

Temos que a Energia cinética é:

T = Σ 1 2 I - ω 2

T = 1 2 π ρ t 2 r A 4 ω A 2 + r B 4 ω B 2 + r C 4 ω C 2 = 1 2 π ρ t 2 r A 4 ω A 2 + r B 4 r A r B 2 ω A 2 + r C 4 r A r C 2 ω A 2

T = 1 2 π ρ t ω A 2 2 r A 2 r A 2 + r B 2 + r C 2

Lembre-se disso

m A = π r A 2 t ρ             e escrever

Eq. (1) como:

T = 1 4 π r A 2 t ρ r A 2 + r B 2 + r C 2

T = 1 4 ω A g r A 2 1 + r B r A 2 + r C r A 2 ω A 2

Passo 3

Dados:

ω A = 150   rpm 2 π 60 = 5 π   rad/s

ω A = 12   lb ,             r A = 8   in . ,           r B = 6   in . ,             r C = 4   in .

M = 60   lb ∙ in . = 5   ft ∙ lb

Passo 4

Trabalho:

U 1 - 2 = M θ = 5   ft ∙ lb θ

Princípio de trabalho e energia para o sistema:

T 1 + U 1 → 2 = T 2

0 + 5 θ = 1 4 12   lb 32.2 8 12 ft 2 1 + 6   in . 8   in . 2 + 4   in . 8   in . 2 5 π 2

5 θ = 0.041408 1 + 4 9 + 1 4 5 π 2

5 θ = 18.518

θ = 3.704   rad rev 2 π   rad = 0.5894   rev

Resposta

θ = 0.589   rev

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando a relação dada no Problema 18.121, determine o período de precessão do pólo norte da Terra em torno do eixo de simetria da Terra. A terra pode ser aproximada por um esferóide oblato de momento
Mostre que para um corpo axissimétrico sem força, as taxas de precessão e spin podem ser expressas, respectivamente, como φ ˙ = H G I ' E ψ ˙ = H G c o s ⁡ θ I ' - I I I ' onde HG é o valor constante
Resolva o problema 18.125 assumindo que propulsores A e D (em vez de A e B) são ativos por 2s
Usando os resultados obtidos nos Problemas 18.143 e 18.144, mostram que para um corpo axissimetrico fixado em seu centro de massa O e sob nenhuma força diferente de seu peso e a reação em 0, o elipsói
Um disco homogêneo de massa é conectado em A e B a um eixo com extremidade em garfo de massa desprezível, que é suportado por um rolamento em C. O disco está livre para girar em torno de seu diâmetro