Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 10

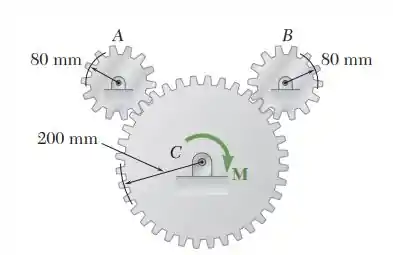
Resolva o Problema, considerando que a binário 10 N ∙ m é aplicado na engrenagem B.

Passo 1

E ai gurizada tudo belezinha??? O exercício pede que a gente resolva o Problema, considerando que a binário 10 N ∙ m é aplicado na engrenagem B.

Momentos de Inércia:

Engrenagens A e B: I A = I B = m k 2 = 2.4 0.06 2 = 8.64 × 10 - 3 K g ∙ m ²

Engrenagem C: I C = 12 0.15 2 = 270 × 10 - 3   K g ∙ m ²

Passo 2

Cinemática: r A ω A = r B ω B = r C ω C

ω A = ω B = 200 80 ω C = 2.5 ω C

θ A = θ B = 2.5   θ C

Energia Cinética: T = 1 2   I   ω 2 :

Passo 3

Posição 1: ω C = 100   r p m = 100 3   π   r a d / s

ω A = ω B = 250   r p m = 25 3   π   r a d / s

Engrenagem A: ( T 1 ) A = 1 2   8.64 × 10 - 3 25   π 3 = 2.9609   J

Engrenagem B: ( T 1 ) B = 1 2   8.64 × 10 - 3 25   π 3 = 2.9609   J

Engrenagem C: ( T 1 ) C = 1 2   270 × 10 - 3 10   π 3 = 14.8044   J

Sistema: T 1 = ( T 1 ) A + ( T 1 ) B + ( T 1 ) C = 20.726   J

Passo 4

Posição 2: ω C = 450   r p m = 15   π   r a d / s

ω A = ω B = 37.5     π   r a d / s

Engrenagem A: ( T 2 ) A = 1 2   8.64 × 10 - 3 37.5   π ² = 59.957   J

Engrenagem B: ( T 2 ) B = 1 2   8.64 × 10 - 3 37.5   π ² = 59.957   J

Engrenagem C: ( T 2 ) C = 1 2   270 × 10 - 3 15   π ² = 299.789   J

Sistema: T 2 = ( T 2 ) A + ( T 2 ) B + ( T 2 ) C = 419.7   J

Trabalho de casal: U 1 → 2 = M θ C = 10   θ C

Princípio de trabalho e energia para o sistema:

T 1 + U 1 → 2 = T 2 :             20.726 + 10 θ C = 419.7

θ C = 39.898   r a d i a n o s

Passo 5

(a)Rotação da Engrenagem C: θ C = 39.898 2.5 = 15.959   r a d i a n o s

Rotação da Engrenagem A: θ A = θ B = 39.898   r a d i a n o s

Princípio de trabalho e energia para equipamentos A:

( T 1 ) A + M A θ A = ( T 2 ) A   :             2.9609 + M A 39.898 = 59.957

M A = 1.4285   N ∙ m

Passo 6

(b)Força tangencial na engrenagem A:

  1. F 1 = M A r A = 1.4285 0.08 = 17.86   N

    2. Respostas

    a) θ C = 2.54   r e v

  2. F 1 = 17.86   N

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para um corpo axissimétrico sem nenhuma força, prove (a) que a taxa de precessão retrógrada nunca pode ser menor que duas vezes a taxa de rotação do corpo em torno de seu eixo de simetria, (b) que na
Uma placa retangular homogênea de massa m nos lados c e 2c é mantida em A e B por um eixo com extremidade em garfo de massa desprezível, que é suportado por um rolamento em C. A placa está livre para
Uma esfera sólida de raio c = 3 pol. é presa como mostrado a um cabo AB de comprimento de 15 pol. A esfera gira em torno de seu diâmetro BC e precessa em torno do eixo vertical AD. Sabendo que θ = 20
Um disco homogêneo de raio de 180 mm é soldado a uma haste AG de comprimento 360 mm e de massa desprezível, que é conectada por uma manilha a um eixo vertical. A haste e o disco podem girar livremente
Consulte os Problemas 18.143 e 18.144.(a) Mostre que a curva (chamada pc / bode) descrita pela ponta do vetor ω em relação a um referencial que coincide com os principais eixos de inércia do corpo ríg