Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 9

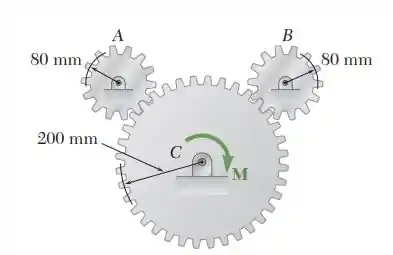
Cada uma das engrenagens A e B tem uma massa de 2,4 kg e um raio de giração de 60 mm, enquanto a engrenagem C tem uma massa de 12 kg e um raio de giração de 150 mm. Um binário M de intensidade 10 N ∙ m é aplicado à engrenagem C. Determine (a) o número de revoluções da engrenagem C necessárias para sua velocidade angular aumentar de 100 para 450 rpm, (b) a força tangencial correspondente que age sobre a engrenagem A.

Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente Determine (a) o número de revoluções da engrenagem C necessárias para sua velocidade angular aumentar de 100 para 450 rpm, (b) a força tangencial correspondente que age sobre a engrenagem A

Passo 2

Momentos de Inércia:

Engrenagens A e B: I A = I B = m k 2 = 2.4 0.06 2 = 8.64 × 10 - 3 K g ∙ m ²

Engrenagem C: I C = 12 0.15 2 = 270 × 10 - 3   K g ∙ m ²

Cinemática: r A ω A = r B ω B = r C ω C

ω A = ω B = 200 80 ω C = 2.5 ω C

θ A = θ B = 2.5   θ C

Passo 3

Energia Cinética: T = 1 2   I   ω 2 :

Posição 1: ω C = 100   r p m = 10 3   π   r a d / s

ω A = ω B = 250   r p m = 25 3   π   r a d / s

Engrenagem A: ( T 1 ) A = 1 2   8.64 × 10 - 3 25   π 3 = 2.9609   J

Engrenagem B: ( T 1 ) B = 1 2   8.64 × 10 - 3 25   π 3 = 2.9609   J

Engrenagem C: ( T 1 ) C = 1 2   270 × 10 - 3 10   π 3 = 14.8044   J

Sistema: T 1 = ( T 1 ) A + ( T 1 ) B + ( T 1 ) C = 20.726   J

Passo 4

Posição 2: ω C = 450   r p m = 15   π   r a d / s

ω A = ω B = 37.5     π   r a d / s

Engrenagem A: ( T 2 ) A = 1 2   8.64 × 10 - 3 37.5   π ² = 59.957   J

Engrenagem B: ( T 2 ) B = 1 2   8.64 × 10 - 3 37.5   π ² = 59.957   J

Engrenagem C: ( T 2 ) C = 1 2   270 × 10 - 3 15   π ² = 299.789   J

Sistema: T 2 = ( T 2 ) A + ( T 2 ) B + ( T 2 ) C = 419.7   J

Trabalho de casal: U 1 → 2 = M θ C = 10   θ C

Princ��pio de trabalho e energia para o sistema:

T 1 + U 1 → 2 = T 2 :             20.726 + 10 θ C = 419.7

θ C = 39.898   r a d i a n o s

Passo 5

(a)Rotação da Engrenagem C:

Rotação da Engrenagem A: θ A = ( 2.5 ) ( 39.898 ) = 99.744   r a d i a n o s

Passo 6

Princípio de trabalho e energia para equipamentos A:

( T 1 ) A + M A θ A = ( T 2 ) A   :             2.9609 + M A 99.744 = 59.957

M A = 0.57142   N ∙ m

(b)Força tangencial na engrenagem A:

F 1 = M A r A = 0.57142 0.08 = 7,14   N

Resposta

  1. θ C = 6.35   r e v

  2. F 1 = 7.14   N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cubo sólido do lado c = 80 mm é preso como mostrado ao cabo AB. Observa-se que gira a uma taxa ψ ˙ = 40 r a d / s em torno de sua diagonal BC e precessa a uma taxa constante ϕ ˙ = 5 r a d / s em to
Um satélite de 2500 kg tem 2,4 de altura e bases octogonais com lados de 1,2 m. Os eixos de coordenadas mostrados são os principais eixos centróides de inércia do satélite, e seus raios de giração são
Mostre que o vetor de velocidade angular w de um corpo axissimétrico sob nenhuma força é observado a partir do próprio corpo girando em torno do eixo de simetria a uma taxa constante n = I ' - I I ' ω
Um satélite geoestacionário de 800 libras está girando com uma velocidade angular ω 0 = ( 1.5 r a d / s ) j quando é atingido em B por um meteorito de 6 onças viajando com uma velocidade v 0 = - ( 160
(a) Aplicando o princípio de conservação de energia, deduza uma terceira equação diferencial para o movimento geral do topo do Problema 18.139. (b) Eliminando as derivadas ϕ ˙ e ψ ˙ da equação obtida