Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 98
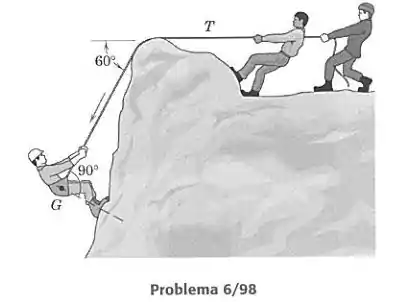
O alpinista de 80 kg é abaixado por sobre a borda do penhasco por seus dois companheiros, que exercem juntos uma força horizontal de 350 N na corda. Calcule o coeficiente de atrito entre a corda e a rocha.
Passo 1
Devemos ser capazes de achar o coeficiente de atrito através da fórmula para o equilíbrio de uma corda em volta de uma superfície, dada por:
Sendo e as trações maior e menor nas extremidades da corda, o coeficiente de atrito entre a corda e a superfície e o ângulo total de giro da corda. Como a fórmula não envolve um raio específico, a superfície não precisa ser circular (como numa polia), e esse ângulo nesse caso é igual a .
Passo 2
O alpinista é equilibrado pela tração feita pelos companheiros e pelo atrito da corda com a superfície rochosa, então a tração menor é a de 350 N feita pelos dois e a tração maior é a força que equilibra o homem. Essa força é descoberta pelo diagrama de corpo livre do alpinista. Temos atuando sobre ele a força peso, a força aplicada pelo solo e a tração . Como há três forças atuando no homem, pelo equilíbrio as linhas de ação das três devem passar pelo mesmo ponto, que é o centro de massa :
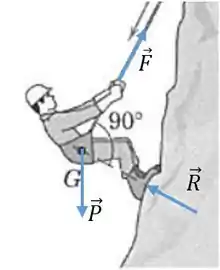
A inclinação de em relação à horizontal é de então pela geometria do desenho a de será então de . Então fazemos os equilíbrios vertical e horizontal do homem para encontrar . Primeiro o horizontal:
Agora o vertical, sabendo que a massa do homem é de 80 kg:
Substituímos por :
Passo 3
Agora que temos todos os valores, substituímos na fórmula do equilíbrio da corda para achar :
Temos , e . Então: