Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 121

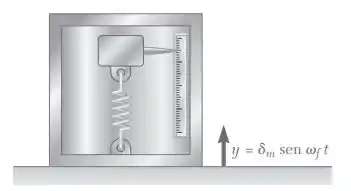
19.120. Um medidor de vibração, usado para medir a amplitude das vibrações, consiste de uma caixa contendo um sistema massa-mola com frequência natural conhecida de 120 Hz. A caixa está rigidamente ligada a uma superfície que está se movendo de acordo com a equação y = δ m sin ⁡ ω f t . Se a amplitude zm do movimento da massa relativo à caixa é usada como uma medida da amplitude m da vibração da superfície, determine (a) o erro percentual quando a frequência da vibração é de 600 Hz, (b) a frequência na qual o erro é zero.

Passo 1

Beleza, vamos resolver esse problema. Vamos ter três movimentos diferentes aqui pra considerar, o primeiro movimento é o movimento vibratório que o equipamento está medindo, vamos chamar esse movimento de y . O segundo movimento é o movimento da massa dentro da caixa, vamos chamar esse movimento de x . O último movimento é o movimento relativo entre os movimentos x e y . O que vai ajudar bastante a gente é que já sabemos uma equação para todos esses movimentos.

O movimento em y é dado no enunciado:

y = δ m sin ⁡ ω f t

O movimento em x a gente encontra no livro:

x = δ m 1 - ω f ω n 2 sin ⁡ ω f t

E o movimento em z é:

z = x - y

Ou

z = δ m 1 - ω f ω n 2 sin ⁡ ω f t - δ m sin ⁡ ω f t

Que é a mesma coisa que

z = δ m 1 - ω f ω n 2 - δ m sin ⁡ ω f t

Então

z m = δ m 1 - ω f ω n 2 - δ m

Passo 2

Agora vai ficar fácil. Vamos começar com o item (a). O erro percentual da frequência quando ω f = 600   H z .

Podemos calcular o erro percentual assim

P = z m δ m - 1

Vamos substituir z m

P = δ m 1 - ω f ω n 2 - δ m ⋅ 1 δ m - 1

Isso fica

P = 1 1 - ω f ω n 2 - 1 - 1

Agora vamos substituir os valores

P = 1 1 - 600 120 2 - 1 - 1

P = 1 1 - 25 - 1 - 1 = 0,0417

Então o erro é

P = 4,17 %

Passo 3

Agora vamos para o item (b). A frequência para o qual o erro é zero. Então temos

0 = z m δ m - 1

Isso significa que

z m = δ m

Então

δ m 1 - ω f ω n 2 - δ m = δ m

Dividindo tudo por δ m

1 1 - ω f ω n 2 - 1 = 1

Agora só precisamos isolar ω f

1 1 - ω f ω n 2 = 2

Então

1 = 2 - 2 ω f ω n 2

Logo

ω f ω n 2 = 1 2

Finalmente temos

ω f = 1 2 ω n

Substituindo ω n

ω f = 1 2 120 = 84,853   H z

Resposta

a : 4,17 % b : 84,853   H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera uniforme de raio r rola para baixo sobre o plano inclinado mostrado na figura sem deslizar. Ela atinge uma superfície horizontal e, após deslizar por um momento, começa a rolar novamente. C
Uma barra delgada AB de comprimento L está em livre com uma velocidade v0 quando a corda AC se torna subitamente esticada. Considerando que o impacto é perfeitamente plástico, determine a velocidade a
Para a viga do Problema 17.117, determine a velocidade da bala de 30 g para que o ângulo máximo de rotação da viga seja de 90°.PROBLEMA 17.117 Uma bala de 30 g é disparada com uma velocidade horizonta
Um bloco retangular uniforme mostrado na figura está se movendo ao longo de uma superfície com velocidade v - 1 quando bate em uma pequena obstrução em B. Considerando que o impacto entre o canto A e
Um barra delgada de comprimento L e massa m é liberada do repouso na posição mostrada na figura. Observa-se que, após a barra bater na superfície vertical, ela ricocheteia e forma um ângulo de 30° com