Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 114

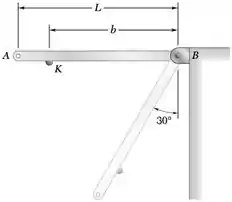
Um barra delgada de comprimento L e massa m é liberada do repouso na posição mostrada na figura. Observa-se que, após a barra bater na superfície vertical, ela ricocheteia e forma um ângulo de 30° com a vertical. (a) Determine o coeficiente de restituição entre a saliência k e a superfície. (b) Mostre que o mesmo rebote pode ser esperado para qualquer posição da saliência k.

Passo 1

Para a análise do balanço para baixo da haste antes do impacto e para o balanço para cima após o impacto, use o princípio de conservação de energia.

Antes do impacto.

V 1 = 0

V 2 = - W L 2 = - m g l 2

T 1 = 0

T 2 = 1 2 I - ω 2 2 + 1 2 m v - 2 2 = 1 2 1 12 m L 2 v 2 2 + 1 2 m 1 2 ω 2 2 = 1 6 m L 2 ω 2 2

T 1 + V 1 = T 2 + V 2 :               0 = 1 6 m L 2 ω 2 2 = - m g L 2 ;                 ω 2 2 = 3 g L                 ω 2 = 1.73205 g L

Passo 2

Depois do impacto.

V 3 = - W L 2 = - m g L 2

V 3 = - W L 2 = cos ⁡ 30 °

T 3 = 1 2 I - ω 3 2 + 1 2 m v - 3 2 = 1 2 1 12 m L 2 ω 3 2 + 1 2 m 1 2 ω 3 2 = 1 6 m L 2 ω 3 2

T 4 = 0

T 3 + V 3 = T 4 + V 4 :               1 6 m L 2 ω 3 2 - m θ L 2 = 0 - m g L 2 cos ⁡ 30 °

ω 3 2 = 1 - cos ⁡ 30 ° g L

ω 3 = 0.63397 g L

Passo 3

Análise de impacto.

Seja r a distância BK.

Antes do impacto,

v k 3 = r ω 3 →   = 1.73205 r g L →

Depois do impacto,

v k 4 = r ω 4 ←   = 0.63397 r g L ←

Coeficiente de restituição.

e = v k 4 n v k 3 n

e = 0.63397 1.73205

Resposta

e = 0.366

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um motor de 100 kg é suportado por quatro molas, cada uma de constante k = 90 kN/m, e está ligado ao chão por um amortecedor que tem coeficiente de amortecimento c = 6.500 N s/m. O motor é restringido
Um motor de 50 kg é parafusado a uma viga leve horizontal que temuma deflexão estática de 6 mm devido ao peso do motor. O desbalanceamento do motor é equivalente a uma massa de 100 g localizado a75 mm
Um excitador de massa excêntrica contrarotativo consiste de duas massas rotativas de 400 g que descrevem círculos de raio 150 mm com amesma velocidade, mas em sentidos opostos, e é colocado em um elem
Um elemento de máquina é suportado por molas e está ligado a umamortecedor como mostrado na figura. Mostre que, se uma força periódica de intensidade P = P ms e nω ƒ t , ƒ é aplicada ao elemento, a am
Um modelo simplificado de uma máquina de lavar é mostrada na figura. Uma trouxa de roupa molhada forma uma massa m b de 10 kg na máquina e causa um desbalanceamento rotativo. A massa rotativa é 20 kg