Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 115

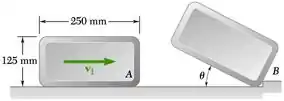
Um bloco retangular uniforme mostrado na figura está se movendo ao longo de uma superfície com velocidade v - 1 quando bate em uma pequena obstrução em B. Considerando que o impacto entre o canto A e obstrução B é perfeitamente plástico, determine a intensidade da velocidade v - 1 para que o máximo ângulo θ que o bloco irá girar seja 30°.

Passo 1

O enunciado pede que a gente determine a intensidade da velocidade v - 1 para que o máximo ângulo θ que o bloco irá girar seja 30°.

Seja m a massa do bloco.

Dimensões:

a = 0   in .   = 0.83333   ft

b = 5   in .   = 0.41667   ft

Passo 2

Momento de inércia em torno do centro de massa.

I - = 1 12 m a 2 + b 2

Seja d a metade da diagonal.

d = 1 2 a 2 + b 2 = 0.46585   ft

Cinemática. Antes do impacto

v - 1 = v 1 → ,                 ω 1 = 0

Passo 3

Após o impacto, o bloco está girando sobre o canto em B.

ω 2 = ω 2               v 2 = d ω 2 ↗

Passo 4

+ Momentos sobre B:

m v 1 b 2 + 0 = I - ω 2 + m d v 2

1 2 m v 1 b = 1 12 m a 2 + b 2 ω 2 + m d 2 ω 2 = 1 3 a 2 + b 2 ω 2

Velocidade angular depois do impacto

ω 2 = 3 v 1 b 2 a 2 + b 2

O movimento após o impacto é uma rotação em torno do canto B.

Posição 2 (imediatamente após o impacto).

v - 2 = d ω 2

Posição 3

θ = 30 °

β = tan - 1 b a = tan - 1   0.5 = 26.565 °

h = d sin ⁡ β + 30 ° = 0.46585 sin ⁡ 56.565 ° = 0.38876   ft

ω 3 = 0                   v - 3 = 0

Passo 5

Energia potencial:

V 2 = m g b 2               V 3 = m g h

Energia cinética:

T 2 = 1 2 I - ω 2 2 + 1 2 m v - 2 2 = 1 2 I - + m d 2 ω 2 2 = 1 6 m a 2 + b 2 ω 2 2                 T 3 = 0

Princípio da conservação de energia:

T 2 + V 3 = T 3 + V 3

1 6 m a 2 + b 2 ω 2 2 + m g b 2 = 0 + m g h

ω 2 2 = 3 g 2 h - b a 2 + b 2 = 3 32.2 0.77751 - 0.41667 0.83333 2 + 0.41667 2 = 40.156   r a d / s 2

ω 2 = 6.3369   rad/s  

Passo 6

Magnitude da velocidade inicial.

Resolvendo a Eq. (1) para v1

v 1 = 2 a 2 + b 2 ω 2 3 b

v 1 = 2 0.83333 2 + 0.41667 2 6.3369 3 0.41667

v 1 = 8.80   ft/s

Resposta

v 1 = 8.80   ft/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra uniforme de massa m é suportada por um pino em A e uma mola de constante k em B e está ligada em D a um amortecedor de coeficiente de amortecimento c. Determine, em termos de m, k e c, para
Uma barra uniforme de 2 kg é suportada por um pino em O e poruma mola em A e está ligada a um amortecedor em B. Determine (a)a equação diferencial do movimento para pequenas oscilações, (b) oângulo qu
Um bloco A de 4 kg é solto de uma altura de 800 mm sobre um bloco B de 9 kg que está em repouso. O bloco B é suportado por uma mola de constante k = 1.500 N/m e está unido a um amortecedor de coeficie
Um motor de 15 kg é suportado por quatro molas, cada uma de constante 45 kN/m. O desbalanceamento do motor é equivalente a umamassa de 20 g localizada a 125 mm do eixo de rotação. Sabendo que omotor é
Mostre que, para um fator de amortecimento c / c c, pequeno, a amplitude máxima de uma vibração forçada ocorre quando ω ƒ ≈ ω n ƒ e queo valor correspondente do fator de ampliação é 1 2 ( c / c c ) .