Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 213
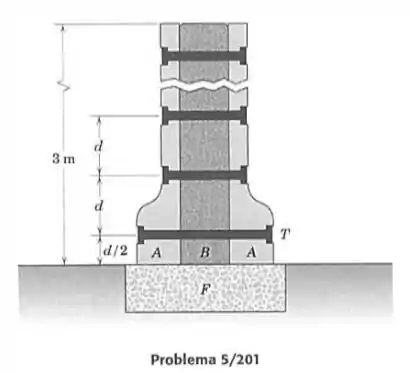
201- Os elementos de um novo método para construção das paredes de fundações de concreto para casas novas estão mostrados na figura. Uma vez que a sapata , está no seu lugar, formas de poliestireno , são erguidas e uma mistura de concreto, , é vertida entre as formas. Os tirantes, , impedem que as formas se separem. Após o concreto curar, as formas são deixadas em seu lugar como isolantes. Como um exercício de projeto, faça uma estimativa conservadora para o espaçamento uniforme,, dos tirantes se a força trativa em cada tirante não deve exceder . O espaçamento horizontal dos tirantes é o mesmo que o espaçamento vertical. Apresente qualquer hipótese levantada. A massa específica do concreto úmido é .
Passo 1
A parede de de concreto faz uma pressão total:
Passo 2
Considerando a área de cada tirante constante temos que ela deve ter uma área máxima de:
Utilizamos a força máxima que ela deve aguentar.
Passo 3
Considerando que a parede tem uma seção quadrada, temos que seu lado de área deve ser de:
O que nos dá uma estimativa conservadora do espaçamento de cada tirante.