Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.12 - Ex. 135

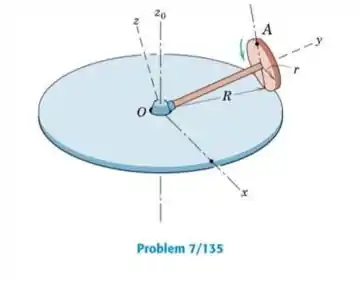
O disco circular de raio r está montado no eixo, que é articulado em O de modo que possa girar em torno do eixo vertical z 0 . Se o disco rola com velocidade constante sem deslizar e realiza uma volta completo ao redor do círculo de raio R no tempo τ , determine a expressão para a velocidade angular absoluta ω do disco. Utilize os eixos x-y-z que giram em torno do eixo z 0 . (Sugestão: A velocidade angular absoluta do disco é igual à velocidade angular em relação aos eixos adicionada (vetorialmente) à velocidade angular em relação aos eixos, conforme observada mantendo x-y-z fixos e girando o disco circular de raio R à taxa de 2 π τ .)

Passo 1

Primeiro vamos determinar a velocidade do referencial que está girando com o disco maior:

Ω → = Ω s e n θ j ^ + c o s θ k ^ = 2 π τ ( s e n θ j ^ + c o s θ k ^ )

Sendo θ o ângulo formado entre a haste que liga o centro dos dois discos e o plano horizontal (plano do disco maior).

Passo 2

Vamos então considerar a velocidade angular do disco menor relativa ao referencial que está girando. Para isso vamos considerar um ponto C que se encontra na borda do disco menor, em contato com o disco maior, a velocidade desse ponto em relação ao referencial que gira será:

v r e l = Ω R = R 2 π τ

Ou seja, ela terá a mesma velocidade linear que o disco maior, por estarem ligados.

Passo 3

Agora escrevemos a velocidade angular relativa:

ω → r e l = v r e l r - j ^ = - R r 2 π τ j ^

Passo 4

Como a velocidade angular absoluta é a soma da velocidade angular dos eixos com a velocidade angular em relação aos eixos:

ω → = 2 π τ - R r j ^ + s e n θ j ^ + c o s θ k ^

Escrevendo e seno e o cosseno do ângulo em termos dos comprimentos (lembrando que R que é a hipotenusa, r um dos catetos e a haste será o outro cateto, R 2 - r 2 :

c o s θ = R 2 - r 2 R

s e n θ = r R

Substituindo, ficamos com:

ω → = 2 π τ r R - R r j ^ + R 2 - r 2 R k ^

Resposta

ω → = 2 π τ r R - R r j ^ + R 2 - r 2 R k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra esbelta uniforme de comprimento l e massa m está soldada ao eixo, que gira apoiado nos mancais A eB com um velocidade angular constante ω . Determine a espressão para a força suportada pelo ma
O mecanismo para controlar a implantação de um painel solar de uma nave espacial a partir da posição A para a posição B está sendo projetado. Determine a expressão vetorial para o único ângulo θ de ro
Se a velocidade angular p do disco do Prob.7/31 está aumentando na taxa de 6 rad/s por segundo e se Ω permanece constante em 4 rad/s, determine a aceleração angular α do disco no instante em que p ati
O helicóptero está baixando o nariz na taxa constante q rad/s. Se as hélices do rotor giram na velocidade constante p rad/s, escreva a expressão para a aceleração angular α do rotor. Suponha que o eix
O pequeno motor M é articulado em relação ao eixo x através de O e transmite ao seu eixo AO uma velocidade constante p rad/s no sentido mostrado, em relação á sua carcaça. O conjunto inteiro é, em seg