Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 143
O disco circular uniforme de está em repouso na posição quando um momento constante no sentido anti-horário é aplicado para rolar o disco para cima na superfície circular. Se o disco rola sem deslizar, calcule a velocidade de seu centro quando a posição mais alta é atingida.
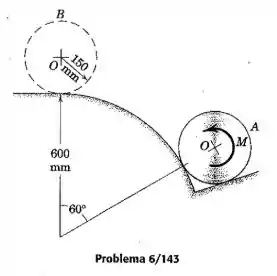
Passo 1
Analisando a figura, é possível notar que o arco pode ser expresso por
De onde tiramos que
Por geometria, sabe-se que o ângulo externo é igual a soma dos ângulos internos não adjacentes. Logo,
Para , temos
Passo 2
Sabemos que
e que
Para a variação da energia cinética
Por fim, para a variação da energia potencial, temos
Como
Retomando a equação que relaciona trabalho e energia, temos
Resposta
Exercícios de Livros Relacionados
3/133) Uma vez em curso a uma velocidade constante , o elevador A de 1000k g sobe á taxa de 1 andar de ( 3m ) por segundo . Determine a potência de entrada P e n t na unidade motora M se a eficiência
3/126) Cada um dos dois sistemas é liberado a partir do repouso . Calcule a velocidade v de cada cilindro de 25k g após o cilindro de 20k g ter caído 2m . O cilindro de 10k g do caso (a) é substituído
3/131) Umaforça horizontal constante p = 700N é aplicada ao mecanismo como mostrado . Com a esfera de 14k g inicialmente em repouso sobre seu suporte com θ = 60 ° , calcule a velocidade v da esfera qu
3/124) O terceiro estágio de um foguete lançado verticalmente para cima sobre o pólo norte sobe sem proulsão até uma altitude máxima de 500k m em seguida à queima total do combustível de seu motor . C
Calcule a velocidade horizontal v com que o carrinho de 20k g deve colidir na mola a fim de comprimi-la um máximo de 100m m . A mola é conhecida como uma mola com “endurecimento”, uma vez que sua rigi