Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 137

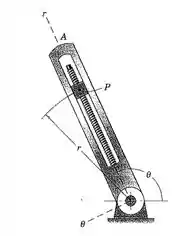
2/137) O movimento do bloco deslizante P na ranhura radial rotativa é controlado pelo parafuso como mostrado . Para o instante representado θ ' = 0,1 r a d / s , θ " = - 0,4 r a d / s 2 e r = 300 m m . Além disso , o parafuso gira a uma velocidade constante fornecendo r ' = 40 m m / s . Para este instante , determine os módulos da velocidade v e da aceleração a de P . Desenhe v e a para θ = 120 ° .

Passo 1

Então galera , a primeira coisa que devemos fazer é achar as componentes da velocidade . Sabemos que :

v r = r ' = 40 m m s

Além disso, temos que :

v θ = r θ ' = 300 0,1 = 30 m m s

Agora para calcularmos o módulo da velocidade basta aplicarmos a fórmula :

v = v r 2 + v θ 2

v = 40 2 + 30 2 = 50 m m / s

Passo 2

Agora para obtermos o módulo da aceleração precisamos achar as suas componentes. Sabemos que :

a r = r " - r θ ' 2  

a r = 0 - 300 0,1 2 = - 3   m m / s 2  

Além disso , temos que :

a θ = r θ " + 2 r ' θ '  

a θ = 300 ( - 0,04 ) + 2 ( 40 ) ( 0,1 ) =   - 4   m m / s 2

Agora para calcularmos o módulo da velocidade basta aplicarmos a fórmula :

a = a r 2 + a θ 2

a = 3 2 + 4 2 = 5 m m / s 2

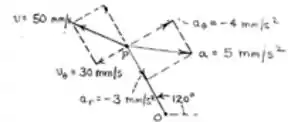
Dêem uma olhada no desenho de a e v para θ = 120 ° :

Resposta

v = 50 m m / s

a = 5 m m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Antes das missões Apollo para a Lua, várias espaçonaves “Lunar Orbiter” foram utilizadas para fotografar a superfície lunar a fim de obter informações a respeito de possíveis locais para pouso. Na con
Deduza a terceira lei do movimento planetário de Kepler das Eqs. (12.39) e (12.45).
Ao aproximar-se do planeta Júpiter, uma nave espacial libera uma sonda que entra na atmosfera do planeta no ponto B a uma altitude de 450 km acima da superfície do planeta. A trajetória da sonda é uma
Um ônibus espacial está descrevendo uma órbita circular a uma altitude de 350 mi acima da superfície da Terra. Quando passa pelo ponto A, ele aciona seu motor por um curto intervalo de tempo para redu
a) Expresse a excentricidade da órbita elíptica descrita por um satélite em torno de um planeta em termos das distâncias r0 e r1 correspondentes, respectivamente, ao perigeu e ao apogeu da órbita. (b)