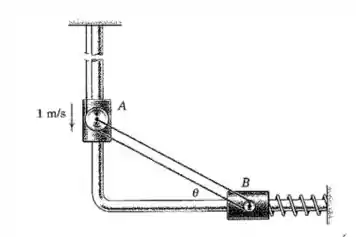
O cilindro tem uma velocidade constante para baixo de . Calcule a velocidade do cilindro para (a) , (b) , (c) . A mola está sob tração durante toda a faixa de interesse do movimento, e as polias estão conectadas pelo cabo de comprimento fixo.
Passo 1
A chave para resolver esse problema está no enunciado: “conectadas por um cabo de comprimento fixo”.
Isso é uma dica muito forte de que precisamos achar uma expressão para o comprimento do cabo. Para isso, vamos dar nome a algumas coisas:
Vamos dizer que é a altura do ponto onde o o cabo do cilindro está preso ao teto, e que é a altura do cilindro em um momento qualquer.
Além disso, vamos dizer que é a distância entre a “curva” e o cilindro .
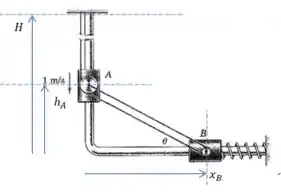
Passo 2
Agora vamos usar a imagem para tentar achar a expressão para o comprimento do cabo.
Repare que o cabo dá duas voltas no trajeto , mas só uma entre o teto e o cilindro , então:
E para expressar o comprimento desse trajeto é só usar o teorema de pitágoras:
Beleza, agora vem a parte importante: vamos derivar essa expressão em relação ao tempo. Quando fizermos isso, todos os termos que são constantes ( e ), vão sumir:
Vamos aplicar a regra da cadeia para calcular a derivada daquela raiz quadrada:
E para resolver aquela derivada do numerador também precisamos usar a regra da cadeia:
E então vamos ficar com a seguinte expressão:
Mas essas derivadas temporais são as velocidades, ou seja: e :
Beleza, já chegamos em uma fórmula interessante.
Passo 3
O objetivo da questão é encontrar para diferentes valores de . Pela figura dá pra ver que:
Então vamos tentar organizar nossa fórmula de forma que aparece um termo como esse.
E agora podemos cortar o :
E isolar o fica bem mais simples:
Beleza, estamos prontos para substituir alguns valores.
Passo 4
Vamos ver o que acontece com a em cada caso:
Então, sabendo que , vamos substituir alguns valores.
(a)
(b)
(c)
Agora sim, conseguimos!
Resposta
(a)
(b)
(c)