Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 51
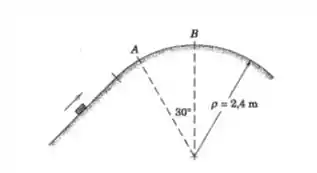
3/51) Se o bloco de passa sobre o topo da porção circular da trajetória com uma velocidade de , calcule o módulo da força normal exercida pela trajetória sobre o bloco . Determine a velocidade máxima que o bloco pode ter em sem que perca o contato com a trajetória .
Passo 1
Bom galera , primeiramente bora analisar as forças que agem sobre o bloco . Usando o princípio do somatório das forças concorrentes , temos que :
Ou seja ,
Substituindo os valores que já conhecemos :
Passo 2
Então pessoal , no limite do bloco perder contato em , temos que :
Sendo assim ,
Resposta
De boa galera? Bora fazer mais exercícios então!
Exercícios de Livros Relacionados
Um veículo é projetado para combinar a sensação de uma motocicleta com o conforto e a segurança de um automóvel. Se o veículo está se movendo a uma velocidade constante de 80 km/h ao longo de uma estr
Determine o coeficiente de atrito estático entre os pneus e a superfície da estrada é μ s = 0,25 , determine a velocidade máxima do carro de 1,5 Mg de modo que ele não deslize quando ele se move na cu
Um avião de 5 Mg está voando com uma velocidade constante de 350 km/h ao longo da trajetória circular horizontal. Se o ângulo de inclinação θ = 15 ° , determine a força de sustentação L atuando sobre
Um bloco liso B, tendo massa de 0,2 kg, está ligado ao vértice A do cone circular reto utilizando uma corda leve. Se o bloco tem velocidade de 0,5 m/s em torno do cone, determine a tração na corda e a
Se a bola tem massa de 30k g e uma velocidade de v = 4m / s no instante em que ela está no ponto mais baixo, θ = 0 ° . Determine a tração da corda e a taxa na qual a velocidade da bola está desacelera