Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 143
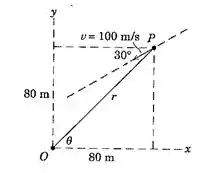
2/143) Quando passa pela posição mostrada , a partícula P tem uma velocidade constante ao longo da linha reta apresentada. Determine os valores correspondentes de , , e .
Passo 1
Bom pessoal , vamos dar uma olhada na figura que ilustra esse problema :
Os vetores velocidade e posição são dados por :
Além disso , nós sabemos que :
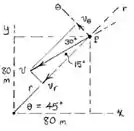
Passo 2
Agora para calcularmos usaremos a relação :
Como , temos que :
Para acharmos , por sua vez , usaremos a fórmula :
Como , temos que:
Resposta
De boa galera? Então vamos para a próxima!
Exercícios de Livros Relacionados
Foi observado que durante o primeiro sobrevoo da Terra feito pela espaçonave Galileu, sua altitude mínima foi de 960 km acima da superfície da Terra. Considerando que a trajetória da espaçonave era pa
Foi observado que durante o seu segundo sobrevoo da Terra, a espaçonave Galileu tinha uma velocidade de 14 × 10 ³ ³ m/s quando atingiu sua altitude mínima de 300 km acima da superfície da Terra. Deter
Para o Problema mostre que F é proporcional à distância r da partícula ao centro de força O.
Um satélite descreve uma trajetória elíptica em torno de um planetade massa M. Representando por r 0 e r 1 , respectivamente, os valoresmínimo e máximo da distância r do satélite ao centro do planeta,
Quando uma sonda espacial, que se aproxima do planeta Vênus em uma trajetória parabólica, atinge o ponto A mais próximo do planeta, sua velocidade é diminuída para que ela seja inserida em uma órbita