Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 149
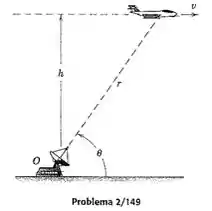
2/149) Um avião a jato voando a uma velocidade constante em uma altitude estásendo rastreado pelo radar localizado em diretamente abaixo da linha de vôo . Se o ângulo está diminuido a uma taxa de quando , determine o valor de neste instante e o módulo da velocidade do avião .
Passo 1
Bom pessoal , a aceleração em todas as direções é zero , então ,
Além disso , sabemos que :
,
Sendo assim , obtemos que :
ou
Resposta
ou
Exercícios de Livros Relacionados
Uma partícula se desloca em uma trajetória circular de 0,3m de raio. Calcule o módulo a da aceleração da partícula(a) se a sua velocidade é constante em 0,6m / s e(b) se a sua velocidade é 0,6m / s ,
Uma sonda espacial deve ser colocada em uma órbita circular de 5600 milhas de raio em torno do planeta Vênus em um plano especificado. Quando a sonda atinge A, o ponto de sua trajetória original mais
Para a sonda espacial do Problema 12.106, sabe-se que r A = 9,3 x10³ mi e que a velocidade da sonda é reduzida para 20.000 ft/s, conforme ela passa por A. Determine (a) a distância do centro de Vênus
A espaçonave Clementine descreveu uma órbita elíptica de altitude mínima hA = 400 km e altitude máxima de hB = 2.940 km acima da superfície da lua. Sabendo que o raio da lua é 1737 km e a massa da lua
Uma sonda espacial em uma órbita baixa da Terra é inserida em uma órbita de transferência elíptica para o planeta Vênus. Sabendo que a massa do sol é 332,8 x 10³ vezes a massa da terra e assumindo que