Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 160

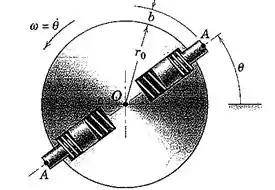
2/160) O disco circular gira em torno de seucentro O com uma velocidade angular constante ω = θ ' e carrega os dois êmbolos com mola mostrados . A distância b que cada êmbolo se projeta a partir da borda do disco variade acordo com b = b 0 sen ⁡ 2 π n t   , onde b 0 é a projeção máxima , n é a freqüência de oscilação constante dos êmbolos nos rasgos radiais , e t é o tempo . Determine os módulos máximos das componentes r e θ da aceleração das extremidades A dos êmbolos durante o seu movimento .

Passo 1

Bom galera , nós já vimos que :

r = r 0 + b 0 sen ⁡ 2 π r t   ,   r ' = 2 π r b 0 cos ⁡ 2 π r t

r =   - 4 π 2 b 0 r 2 sen ⁡ 2 π r t

θ ' = ω 1     ,   θ " = 0

a r = r " - r θ ' 2

Substituindo os valores que conhecemos , obtemos que :

a r = - 4 π 2 b 0 r 2 s e n ⁡ 2 π r t - ( r 0 + b 0 sen ⁡ 2 π r t ) ω 2

a r =   - 4 π 2 r 2 + ω 2 b 0 sen ⁡ 2 π r t - r 0 w 2

a r m a x = 4 π 2 r 2 + ω 2 b 0 + r 0 ω 2

a θ = r θ " + 2 r ' θ '

a θ = 0 + 4 π b 0 r ω cos ⁡ 2 π r t

a θ max ⁡ = 4 π b 0 r ω

Resposta

a r m a x = 4 π 2 r 2 + ω 2 b 0 + r 0 ω 2

a θ max ⁡ = 4 π b 0 r ω

Tranquilo galera? Bora resolver mais questões então!!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2/131) Um piloto decorridas guiando a uma velocidade de 250 k m / h no trecho de pista reta aplica os freios no ponto A e reduz sua velocidade a uma taxa uniforme para 200 k m / h em C em uma distânci
2/129) O carro de corrida A segue a trajetória a-a enquanto o carro de corrida B segue a trajetória b-b sobre a pista sem inclinação . Se cada carro tem uma velocidade constante limitada á corresponde
2/128) Em um determinado ponto na reentrada do ônibus espacial naatmosfera da terra , aaceleração total do ônibus espacial pode ser representada por duas componentes . Uma componente é aacelração grav
2/134) Em um teste de direção , um carro é conduzido através do percurso sinuoso mostrado . Supõe-se que a trajetória do carro é senoidal e que a máxima aceleração lateral é 0,7 g . Se os examinadores
2/130) Uma bola é lançada horizontalmente a partir do topo de um penhasco de 50 m em A com uma velocidade de 15 m / s e cai no ponto C . Devido a um forte vento horizontal , a bola tem uma aceleração