Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 22
22. Uma força é aplicada em uma haste dobrada que é apoiada por um rolete e um suporte com pino. Para cada um dos três casos mostrados, determine as forças internas no ponto :
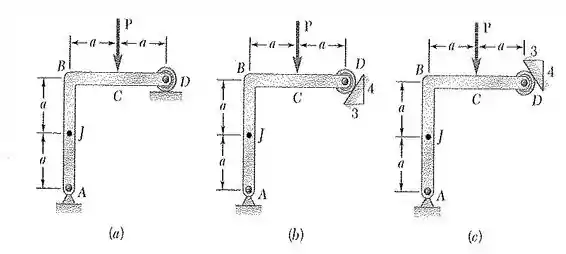
Passo 1
a) Bom! Primeiramente vamos fazer o esboço de todas as forças presentes no nosso sistema , o chamado diagrama de corpo livre:
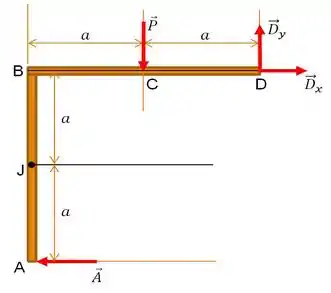
E agora, vamos tratar de fazer o somatório dos momentos em relação a um ponto de nosso interesse. Que tal o ponto ?
Depois, bora fazer o somatório das forças na direção , considerando que o esforço cortante esteja nesta direção. Adotaremos o a convenção do esforço cortante como atuando na horizontal para a direita.
E para descobrir o quanto vale o momento fletor, vamos fazer o esboço do elemento . Repara que utilizamos apenas um pequeno elemento do componente :
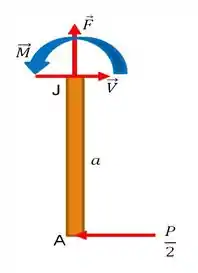
Baseado nisso, façamos o somatório das forças em :
Que belezinha! Não tem força atuante em . Agora, para descobrir o momento fletor, bora fazer o somatório dos momentos em relação ao ponto :
Passo 2
b) Repetiremos os mesmos procedimentos do . Primeiro, o esboço de :
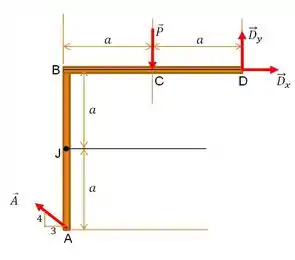
Depois, vamos tratar de fazer o somatório dos momentos em relação a um ponto de nosso interesse. Que tal o ponto ?
E agora que já sabemos a direção de ; para descobrir o quanto vale o esforço cortante e momento fletor, vamos fazer o esboço do elemento :
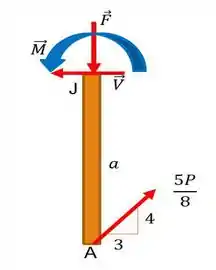
Em seguida, bora fazer o somatório das forças na direção , considerando que o esforço cortante esteja nesta direção. Adotaremos o a convenção do esforço cortante como atuando na horizontal para a esquerda, ou seja, negativo:
E para descobrir o quanto vale o momento fletor, façamos o somatório dos momentos em relação ao ponto :
Não podemos nos esquecer de fazer o somatório das forças em para achar o valor de , né:
Passo 3
c) Essa letra também vai ser só no esquema copiar e colar. A primeira coisa a fazer, é o esboço de :
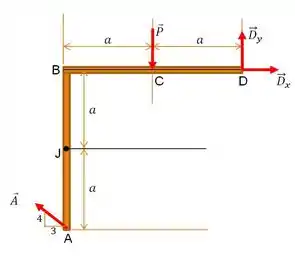
Depois, vamos tratar de fazer o somatório dos momentos em relação a um ponto de nosso interesse. Que tal o ponto ?
Mais adiante, partimos pro cálculo do esforço cortante. Adotaremos o a convenção do esforço cortante como atuando na horizontal para a direita, ou seja, positivo:
Posteriormente, devemos fazer o somatório das forças em :
E por último, para descobrir o quanto vale o momento fletor, façamos o somatório dos momentos em relação ao ponto :
Resposta
a)
b)
c)