Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 52
Uma conexão soldada está em equilíbrio sob a ação de quatro forças como mostra a figura. Sabendo que e , determine as intensidades das outras duas forças.
Passo 1
Tá legal, vamos lá! Antes de começar o exercício, é sempre bom ter em mente as dicas que o próprio livro nos dá antes de cada seção de exercícios, na parte de “metodologia para resolução de problemas”. Então beleza, seguindo aquelas dicas, vamos começar fazendo o diagrama de corpo livre:
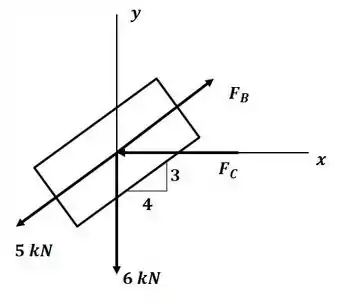
Passo 2
Agora que temos o DCL do problema, e temos 4 forças, sendo duas desconhecidas, vamos decompor as forças nas direções e e aplicar o somatório de forças nessas duas direções. Começando pela direção :
Isolando e resolvendo, temos:
Passo 3
Agora, aplicando o somatório na direção :
Isolando e resolvendo, temos:
Resposta
Exercícios de Livros Relacionados
O centro de flutuação B do casco de um navio é o centroide do seu volume submerso. As seções transversais das áreas submersas A , ao longo da direção transversal do casco do rebocador mostrado, estão
Um cabo, com massa de 15 kg/m, está preso ao ponto A e passa sobre uma pequena polia B, situada sobre a mesma linha horizontal que A. Determine a deflexão h e o comprimento S do cabo entre A e B , se
Um determinado comprimento de um cabo de transmissão está suspenso das duas torres, como mostrado. O cabo tem uma massa de 20 kg por metro. Se a máxima força trativa admissível no cabo vale 75 kN, det
Um cilindro circular de massa específica ρ 1 flutua em um líquido de massa específica ρ 2 . Se d é o diâmetro do cilindro e h é a altura submersa, faça o gráfico da razão r = h / d em função de ρ 1 /
Determine as componentes vertical e horizontal da reação nos pinos A e C da estrutura de dois membros