Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 32
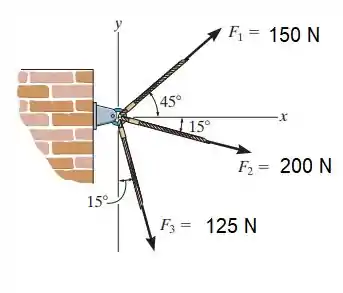
Determine a intensidade da força resultante que atua sobre o pino e sua direção, medida no sentido horário a partir do eixo x positivo.
Passo 1
Para descobrirmos a força resultante vamos decompor todas as forças nos eixos x e y, e depois disso vamos calcular a força resultante nos eixos x e y e por fim poderemos somar vetorialmente a força resultante no eixo x com a força resultante no eixo y, assim teremos a intensidade da força resultante, tal como o exercício pede.
Passo 2
Vamos determinar a intensidade das forças no eixo x
Agora vamos calcular a intensidade da força resultante no eixo x
Passo 3
Agora a gente usa a mesma estratégia para calcular determinar as forças no eixo y
Os valores negativos aparecem nas forças que estão para baixo, ao contrário do eixo y.
Agora vamos calcular a intensidade da força resultante no eixo y
Passo 4
Agora vamos somar vetorialmente as forças em x e em y
Passo 5
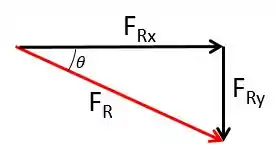
Só falta descobrir o ângulo θ agora.
Repare que dos vetores podemos extrair esse triângulo
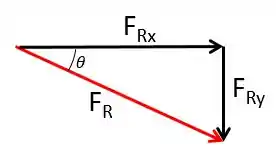
Então são catetos desse triângulo, e como nos diz a trigonometria