Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 234
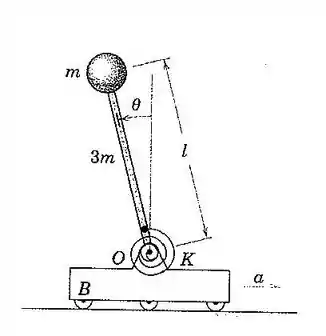
234. O sistema do problema é representado aqui. O carrinho se desloca para a direita com aceleração . Se , e , determine o deslocamento angular em regime permanente da haste esbelta uniforme de massa . Considere a pequena esfera de massa na extremidade como uma partícula. A mola, que exerce um momento de módulo sobre a haste, está sem deformação quando a haste está vertical.
Passo 1
Bom! Hora da malandragem, né galera! Da questão , tiramos que o valor de é dado pela seguinte relação:
E como já temos o valor da constante , da massa , do ângulo e do comprimento , agora é só correr pro abraço e substituir os valores numéricos:
Passo 2
Danou-se! Essa é um tipo de equação que só da pra resolver usando ferramentas lá do cálculo numérico:
Mas podemos fazer algumas gambiarras pra ver se conseguimos arrumar alguma coisa, se é que isso é possível. Bora substituir alguns valores numéricos, e tentar aplicar na nossa equação, o método da bissecção. Consideremos o ângulo em radianos:
Primeiramente, vamos testar os valores e .
Para
Para :
Como os sinais dos dois valores do nosso intervalo, são opostos, sendo que e , temos que há uma raiz nesse intervalo. E seguinte o raciocínio do método da bissecção, vamos dividi-lo ainda mais. Para isso, basta somar os dois valores anteriores e dividimos por dois:
Depois, façamos o teste para :
E o nosso novo intervalo, vai ser . Vamos novamente dividi-lo por dois para encontrar outro valor de :
Fazemos, novamente o teste para :
Como e , a raiz vai estar agora nesse intervalo. A desvantagem dessse processo, e que ele exige um número muito grande de repetições até atingir uma determinada faixa de erro. Por isso, deve ser feito em um computador. A nossa próxima iteração vai ser a que iremos usar para calcular a raiz, até porque ninguém é de ferro, né:
E a raiz da nossa equação, que é o valor do ângulo que queremos, é dado pela divisão do último intervalo que obtemos:
Quer ver só como esse método, apesar das suas limitações, é muito eficaz:
Esse valor é muito próximo de zero. É claro que se fizer esse processo do método da bissecção em mais duas ou três iterações, a raiz encontrada vai ser ainda mais próxima do valor real. O que acha de agora, usarmos outra ferramenta para tentar nos aproximar ainda mais da nossa raiz:
Sabe o Método de Newton! Ele é dado pela seguinte relação:
O ponto do teste () nós já temos, que é aquele último valor que obtivemos pelo método da bissecção, de ou .
Falta agora, apenas calcular a primeira derivada de , que é dada por:
E vamos fazer apenas nossa primeira e única iteração, pelo Método de Newton. Não esqueça que estamos trabalhando com radianos:
Viu só! Quem precisa de computador, rapaz! Conseguimos a raiz quase que exata, do que estávamos procurando.