Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 207
Uma lata de suco congelado está apoiada sobre a prateleira horizontal de uma porta de congelador conforme mostrado. Com que velocidade angular máxima a porta pode ser ‘batida’ contra sua vedação e não desalojar a lata? Suponha que a lata rola sem deslizar sobre a extremidade da prateleira, e despreze a dimensão comparada com a distância de 500 mm.
Passo 1
O enunciado nos dá as seguintes informações:
Distância : ;
Raio da lata: ;
Altura do suporte: .
Devemos determinar a velocidade angular máxima da porta em que a lata não seja desalojada, ou seja, não caia da porta ultrapassando o seu apoio mostrado na figura.
Passo 2
Primeiramente, vamos supor a situação extrema em que a lata fique posicionada em cima do suporte, porém não cai, conforme a ilustração abaixo:
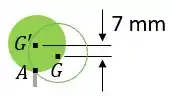
Neste momento, temos que a energia potêncial do instante inicial para o instante final é
Onde
Substituindo na equação principal, obtemos
Passo 3
Agora, em uma segunda hipótese, vamos supor que a lata seja somente empurrada contra o suporte, conforme a ilustração abaixo:
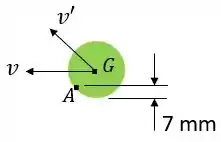
Neste caso, temos que a variação da quantidade de movimento no ponto é nula, logo
Portanto,
Sabemos que , logo, neste problema, temos que
Substituindos os dados na equação principal, temos que