Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas fundamentais - Ex. 06
O carretel tem um peso de 750 N e um raio de giração em relação a seu centro de gravidade . Se ele é submetido a um torque M = 37,5 N.m e parte do repouso quando o torque é aplicado, determine sua velocidade angular em 3 segundos. O coeficiente de atrito cinético entre o carretel e o plano horizontal é .
Passo 1
Começaremos o exercício calculando o momento de inércia do carretel em relação a seu centro de massa:
Passo 2
Agora iremos aplicar o princípio do impulso e quantidade de movimento linear na direção y para descobrir o valor da reação normal, conforme o diagrama a seguir:
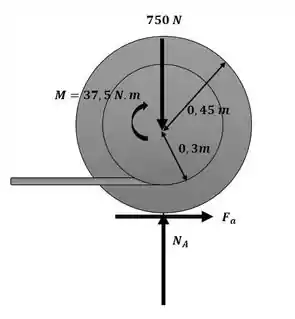
Passo 3
Agora iremos aplicar o princípio do impulso e da quantidade de movimento angular para o sistema ainda com o auxílio do esquema apresentado no passo 2:
Resposta
Exercícios de Livros Relacionados
O ginasta de 75 kg solta a barra horizontal em uma posição completamente deformada A, girando com uma velocidade angular ω A = 3r a d / s . Estime sua velocidade angular quando ele assume uma posição
O carro atinge um poste de luz, o qual é projetado para romper-se em sua base com resistência desprezível. De um vídeo feito da colisão, é observado que o poste foi submetido a uma velocidade angular
O satélite de 200 kg tem um raio de giração em relação ao eixo z centroidal é k z = 1,25m . Inicialmente, ele está girando com uma velocidade angular constante ω 0 = 1500 kr e v / m i n . Se os dois j
Se o eixo é submetido a um torque M = 15 t 2N . m , onde t é dado em segundos, determine a velocidade angular do conjunto quando t = 3 s, partindo do repouso. As barras AB e BC, cada uma, têm uma mass
Se o eixo é submetido a um torque M = 30 e - 0,1 tN . m , onde t é dado em segundos, determine a velocidade angular da montagem qundo t = 5 s, partindo do repouso. A placa retangular tem uma massa de