Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 125

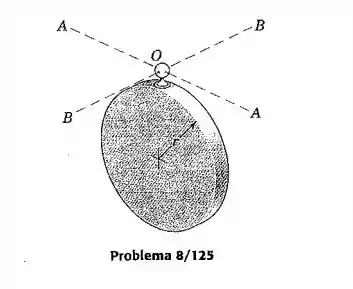
O disco circular uniforme está suspenso por uma cavidade (não mostrada) que se encaixa sobre a pequena esfera de fixação em O . Determine o período para movimentos pequenos, se o disco oscila livremente em torno (a) do eixo A - A e (b) do eixo B - B . Despreze o pequeno deslocamento, massa, e atrito da esfera.

Passo 1

Para esse problema vamos usar as relações de torque resultante e o teorema dos eixos paralelos para encontrar os momentos de inércia em cada eixo.

Passo 2

Vamos começar calculando os momentos de inércia para cada eixo. Temos que para o eixo A - A iremos calcular a integral do disco inicialmente passando pelo centro

∫ - r r x 2 ⋅ d m = 1 4 ⋅ m ⋅ r 2

Aplicando agora o teorema dos eixos paralelos, temos que

I A A = I o A + m ⋅ r 2 = 5 4 ⋅ m ⋅ r 2

Temos que a única força atuante é a peso, dada por m ⋅ g ⋅ r . Assim, temos que o torque resultante será

Τ = I A A ⋅ θ ¨

- m ⋅ g ⋅ r ⋅ sin ⁡ θ = 5 4 ⋅ m ⋅ r 2 ⋅ θ ¨

θ ¨ + 4 ⋅ g 5 ⋅ r ⋅ sin ⁡ θ = 0

Para θ pequeno, temos que sin ⁡ θ → θ . Assim

θ ¨ + 4 ⋅ g 5 ⋅ r ⋅ θ = 0

ω n = 4 ⋅ g 5 ⋅ r = 2 ⋅ g 5 ⋅ r

Passo 3

Fazendo o mesmo processo para B - B , chegaremos que I B B será

I B B = I o B + m ⋅ r 2 = 3 2 ⋅ m ⋅ r 2

Temos que a mesma força será atuante no sistema, então nossa equação para o torque ficará

- m ⋅ g ⋅ r ⋅ sin ⁡ θ = 3 2 ⋅ m ⋅ r 2 ⋅ θ ¨

θ ¨ + 2 ⋅ g 3 ⋅ r ⋅ sin ⁡ θ = 0

Para θ pequeno, temos que sin ⁡ θ → θ . Assim

θ ¨ + 2 ⋅ g 3 ⋅ r ⋅ θ = 0

ω n = 2 ⋅ g 3 ⋅ r

Resposta

  1. ω n = 2 ⋅ g 5 ⋅ r

  2. ω n = 2 ⋅ g 3 ⋅ r
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

72. Comprove que a expressão para x ( t ) na Equação 14.56 é uma solução da equação de movimento para um oscilador amortecido, a Equação 14.55 , se e somente se a frequência angular ω for dada pela ex
13.15E Um oscilador amortecido definido pelos parâmetros ω 0 = 1,00 × 10 6s -1 , γ = 5,00s -1 oscila livremente. A) Que fração de sua energia o oscilador perde em cada ciclo? B) em quantos ciclos o os
13.16P Um oscilador massa-mola forçado tem seu movimento regido pela equação: 50,00g . x ' ' + 5,000 × 10 - 3 N s -1 . x ' + 5,000Ncm¹ . x = 0 ¹ Sendo x 0 = 10cm , v 0 = 0 , calcule a expressão para x
Um ovo de 50,0 g, fervido durante muito tempo, está preso na extremidade de uma mola cuja constante é k = 25,0 N/m. Seu deslocamento inicial é igual a 0,300 m. Uma força de amortecimento Fx = -hvx atu
Um objeto de 1,35 kg é preso a uma mola horizontal com constante de força de 2,5 N/cm. O objeto começa a oscilar puxando-a por 6,0 cm a partir de sua posição de equilíbrio e soltando-a de modo que fiq