Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 27
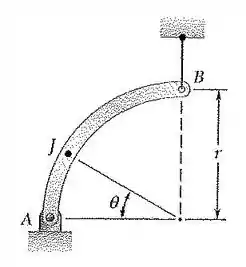
27. Para a haste do problema , determine a intensidade e a localização do momento fletor máximo:
Passo 1
Bom, vamos lá tratar de resolver esse probleminha. Baseado no que já sabemos, qual é a primeira coisa que temos que fazer para dar inicío à solução do nosso exercício?
É isso mesmo que você está pensando! Bora tratar de fazer o diagrama de corpo livre para a nossa haste, tratando de representar todas as forças possíveis:
Feito essa belezinha de desenho, vamos agora analisar as forças e momentos presentes no nosso sistema. Para isso, temos que recorrer a uma ferramenta que com certeza, você já está cansado de saber, o somatório das forças em e e também de momento.
Vamos lá! Primeiramente, vamos tratar de fazer o somatório das forças no eixo , e quem sabe podemos descobrir o quanto vale aquele :
Olha que maravilha! Não tem reação no eixo :
Existem duas maneiras de tentar achar aquele , o somatório das forças em ou o somatório dos momentos em relação a um ponto de nosso interesse. Vamos escolher a segunda opção, porque nos permite trabalhar com menos forças. E em relação ao ponto de interesse, que tal o ponto ?
Passo 2
Como já obtemos o valor das reações no ponto , olha só a próxima coisa que temos que fazer. Vamos separar uma pequena seção do elemento , indo do ponto até um ponto qualquer que chamaremos de . Neste elemento é que vamos poder encontrar o esforço cortante e momento fletor, como representado na imagem abaixo:
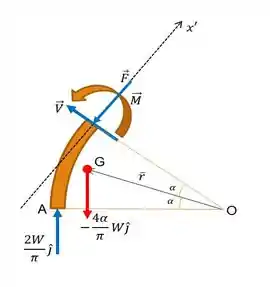
Repara só na imagem! O ângulo do problema é representado como o dobro de :
E de problemas anteriores, estamos carecas de saber que:
Só que como é o peso total do elemento , uma vez que estamos trabalhando apenas com uma seção desse elemento, temos que essa seção vai ser proporcional ao ângulo que temos, de acordo com a seguinte relação:
Passo 3
E então, olhemos novamente a figura:
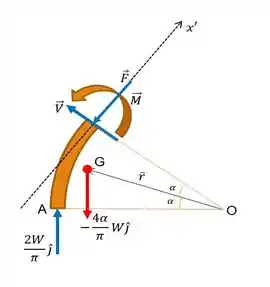
Tá vendo esse eixo aí!! Esse é o eixo da direção tangencial. Vamos fazer o somatório de todas as forças nessa direção e então, obter o valor da força :
E como já sabemos o valor de ; para descobrir o quanto vale o momento fletor, vamos fazer o somatório dos momentos em relação ao ponto :
Só que:
O que nos leva a:
Essa é a nossa expressão final do momento fletor! Coisinha mais complicada, não!? Bom! Lembra lá do Cálculo , a ferramenta que a gente usa para achar o ponto onde determinada expressão adquire valor máximo.
Isso aí mesmo que você está pensando! Temos que tirar a primeira derivada dessa expressãozinha aí do momento e igualá-la a zero. Desse jeito, encontraremos nossa resposta:
E tá na cara que isso aí vai valer zero, quando:
Como obtemos dois valores, vamos testá-los na expressão do momento e ver qual dos dois é o maior:
Para :
Para :
Logo, nosso momento máximo, , é dado por: