Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 71

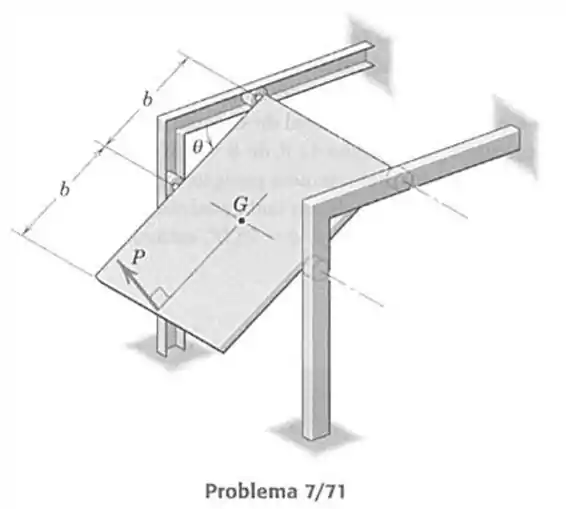
71- O painel retangular uniforme de massa m e centro de massa em G é guiado por roletes- o par superior na guia horizontal e o par inferior na guia vertical. Determine a força P , aplicada a extremidade inferior e normal ao painel, necessária para manter o equilíbrio em um ângulo θ dado. (Sugestão: Para avaliar o trabalho realizado por P , substitua-a por suas componentes horizontal e vertical.)

Passo 1

Vamos desenhar uma visão lateral desse painel e traçar as principais forças e os eixos (que não passam sobre o eixo a ser estudado).

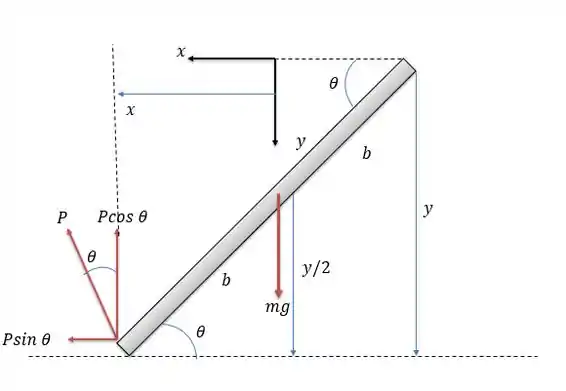
Se considerarmos como origem os eixos selecionados nós teremos como somatória dos trabalhos virtuais:

∑ δ U = 0

O valor de y será dado por:

sin ⁡ θ = y 2 b → y = 2 b sin ⁡ θ

Fazendo a derivada da expressão encontraremos:

δ y = 2 b c o s   θ   δ θ

O valor de x então será:

cos ⁡ θ = x 2 b → x = b cos ⁡ θ

Fazendo a derivada então:

δ x = - b s i n   θ   δ θ

Passo 2

O trabalho virtual realizado pela força peso será:

U w = m g   δ y 2

Onde ela sempre será paralelo a distância de interesse (que sai do eixo e vai até o ponte de aplicação).

O da P c o s   θ :

U 1 = - P c o s   θ   δ y

E o de P s i n   θ :

U 2 = P s i n   θ   δ x

Logo a somatória dos trabalhos será:

m g δ y 2 - P c o s   θ   δ y + P s i n   θ   δ x = 0

Passo 3

Substituindo os valores diferenciais nós teremos:

m g b cos ⁡ θ   δ θ - 2 P c o s   θ b cos ⁡ θ δ θ + P sin ⁡ θ × - b s i n   θ   δ θ = 0

Cortando δ θ .

m g b c o s   θ - 2 b P c o s 2 θ - P b s i n 2 θ = 0

Cortando b .

m g c o s   θ = 2 P c o s 2 θ + P s i n 2 θ

m g c o s   θ = P ( 2 cos 2 ⁡ θ + sin 2 ⁡ θ ) = P ( cos 2 θ ⁡ + cos 2 ⁡ θ + sin 2 ⁡ θ )

P = m g cos ⁡   θ 1 + cos 2 ⁡ θ

Resposta

P = m g cos ⁡   θ 1 + cos 2 ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13- As conexões simétricas sustentam o cilindro de massa m no plano vertical, pela ação dos dois momentos M aplicados a O A e a O B , como mostrado. Determine o valor do momento M em função de θ . A m
14- O macaco portátil é operado por um cilindro hidráulico que controla o movimento horizontal da extremidade A do tirante, no rasgo horizontal. Determine a força compressiva C na barra do pistão do c
16- O redutor de velocidade mostrado está projetado com uma razão de engrenagens de 40 : 1 . Com um torque de entrada M 1 = 30N m , o torque de saída medido vale M 2 = 1180N m . Determine a eficiência
12- Para cada unidade de movimento da extremidade livre da corda na direção da força aplicada P , a carga de 100k g se move em um quarto de unidade. Se a eficiência mecânica e do conjunto de roldanas
15- O guindaste manual é projetado para levantar uma carga de 100k g , sendo que 25 voltas na manivela produzem, através do eixo redutor, uma revolução no tambor. Considerando uma perda de energia de