Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 75

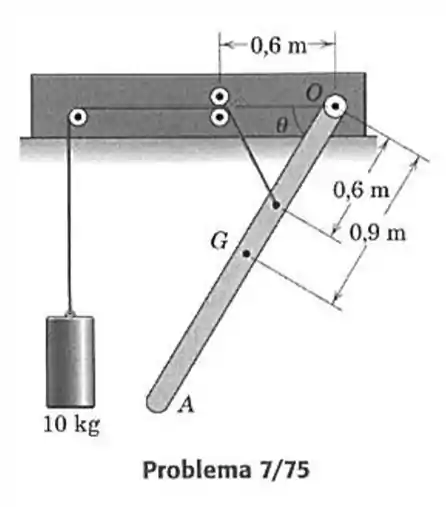
75- A barra O A , que tem uma massa de 25   k g e centro de massa em G , é articulada em torno de sua extremidade O e balança no plano vertical sob a restrição do contrapeso de 10   k g . Escreva a expressão para a energia potencial total do sistema, fazendo V g = 0 quando θ = 0 até 360 . A partir do gráfico dos resultados, determine a posição, ou posições, de equilíbrio e a estabilidade do equilíbrio em cada posição.

Passo 1

Quando θ aumenta a massa de 10   k g sobe de posição, então isso nos dá a analise de apensas duas energias a do trabalho da massa de 10   k g e a energia potencial da barra. E agora olhando como o sistema se comporta da seguinte forma.

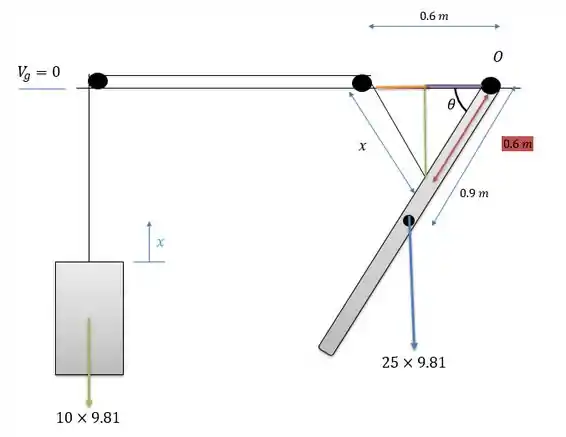
A energia potencial gravitacional da barra pode simplesmente ser calculada ao se rebater a altura da barra no eixo vertical, de forma que achemos sua altura em função de θ , logo a altura da barra será:

h = 0.9 sin ⁡ θ

Logo a energia potencial gravitacional será:

V g = - 25 × 9.81 × 0.9 sin ⁡ θ = - 220.725 sin ⁡ θ

É negativo a energia pois ele encontra-se abaixo da sua base.

Passo 2

Agora para calcular o trabalho nós devemos notar que quando θ = 0 o valor de x = 0 , logo o bloco sobe a medida que x aumenta de forma que o trabalho do bloco será calculado de forma que:

U = 10 × 9.81 × x

Para calcular x foram traçados na figura retas coloridas dentro do triângulo formados entre o cabo de tração do bloco e a barra O G A , tal que temos o triângulo retângulo formado entre a hipotenusa x e o catetos formados entre as retas verde e laranja:

r e t a   r o x a + r e t a   l a r a n j a = 0.6

r e t a   v e r d e = 0.6   s i n θ

r e t a   r o x a = 0.6 cos ⁡ θ

Logo o tamanho da reta laranja será:

r e t a   l a r a n j a = 0.6 - 0.6 cos ⁡ θ = 0.6 ( 1 - cos ⁡ θ )

Passo 3

Agora podemos calcular o valor de x ao fazer Pitágoras.

x 2 = 0.6 2 ( 1 - cos ⁡ θ ) 2 + 0.6 2 sin 2 ⁡ θ

Agora abrindo 1 - c o s θ 2 :

x 2 = 0.6 2 [ 1 - 2 cos ⁡ θ + cos 2 ⁡ θ + sin 2 ⁡ θ ]

x 2 = 0.6 2 [ 2 - 2 cos ⁡ θ ]  

x 2 = 0.6 2 × 2 [ 1 - cos ⁡ θ ]

Pela fórmula trigonométrica do arco metade temos que:

sin ⁡ x 2 = 1 - cos ⁡ x 2 → 1 - cos ⁡ x = 2 sin 2 ⁡ x 2

x 2 = 0.6 2 × 2 2 × sin 2 ⁡ θ 2

Logo x será:

x = 1.2 × sin ⁡ θ 2

Então a equação do trabalho será de:

10 × 9.81 × 1.2 × sin ⁡ θ 2 = 117.72 sin ⁡ θ 2

O que faz com que a equação geral do sistema seja:

V = 117.72 sin ⁡ θ 2 - 220.725 sin ⁡ θ

Resposta

Plotando o gráfico de estabilidade desse sistema nós encontramos:

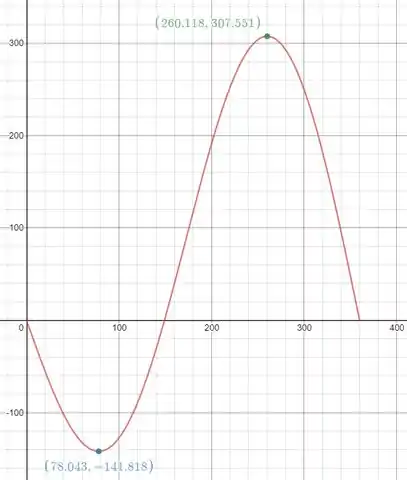
Nós encontramos como ângulos de estabilidade os ângulo θ = 78 ° e θ = 260.1 ° . E como a concavidade para θ = 78 está para cima essa posição será estável, e como a concavidade em θ = 260.1 ° está para baixo o sistema será instável.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento M que deve ser aplicado em O para sustentar o mecanismo na posição θ = 30 ° . As massas do disco em C , da barra O A e da barra B C são m 0 , m e 2 m , respectivamente.
Na morsa acionada por um parafuso, um torque M aplicado à manopla do parafuso aperta a morsa aumentando a distância B D e, portanto, produzindo uma força de aperto C . O parafuso é rosqueado através d
Uma “caixa preta” contém uma série de cremalheiras e pinhões, engrenagens e outros elementos mecânicos internos interconectados, os quais transformam o movimento linear da haste A em um movimento line
A barra leve O C é articulada em O e balança no plano vertical. Quando θ = 0 , a mola de rigidez k não está alongada. Determine o ângulo de equilíbrio, correspondente a uma força vertical P aplicada à
Identifique quais dos itens de ( a ) até ( f ) são mais bem resolvidos ( A ) pelas equações de equilíbrio de força e momento e ( B ) por trabalho virtual. Descreva sucintamente o procedimento para cad