Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 72
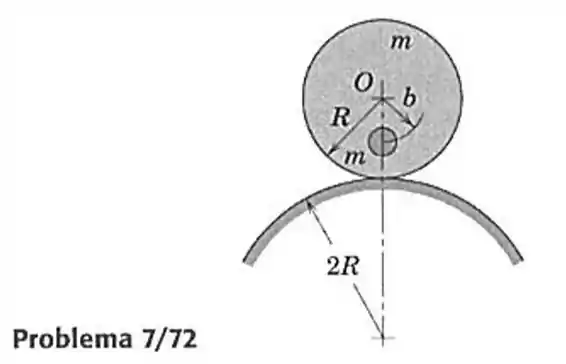
72- O disco uniforme de alumínio com raio e massa rola sem deslizar sobre a superfície circular fixa de raio . Um cilindro de chumbo também de massa está preso ao disco e seu centro está localizado a uma distância do centro do disco. Determine o valor mínimo de para o qual o disco permanecerá em equilíbrio estável no topo, sobre a superfície cilíndrica, como mostrado.
Passo 1
Vamos fazer com que o corpo composto esférico percorra um ângulo em relação ao centro da superfície tal como na figura abaixo.
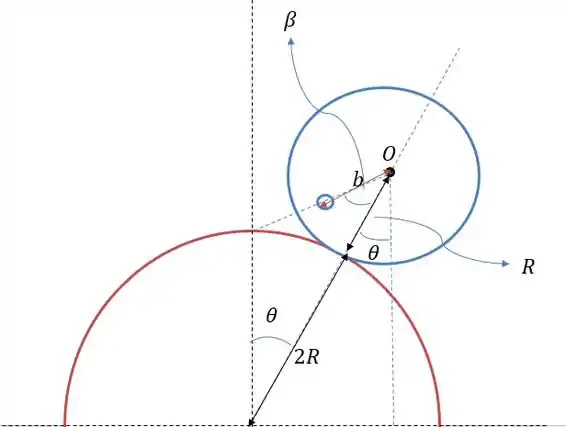
Agora vem um exercício de imaginação, já que os dois tem raios diferentes isso significará que a bola azul percorrerá uma distância bem maior do que caso se ela estivesse em uma superfície plana. Logo além a bola percorrerá um ângulo proporcional a distâncias dos dois raios.
A relação entre os dois ângulos é a distância do arco formado pelo deslocamento do círculo azul que é calculado como:
Passo 2
Agora podemos fazer a somatória das energias potencias das duas bolas compostas.
Para a esfera maior de alumínio temos que a esfera maior não altera suficiente o seu centro de massa logo que continua em logo:
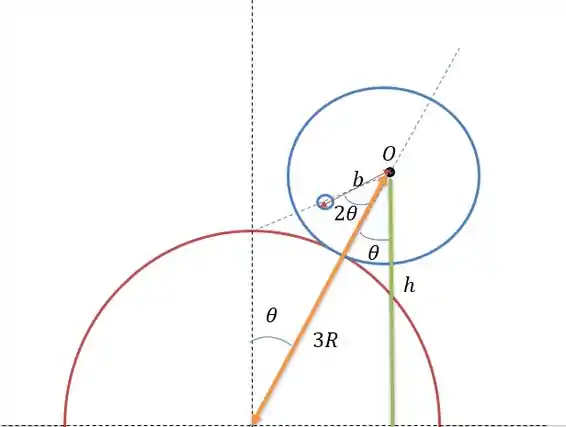
O que faz com que a energia potencial dessa esfera maior seja:
Passo 3
Para a pequena esfera de chumbo:
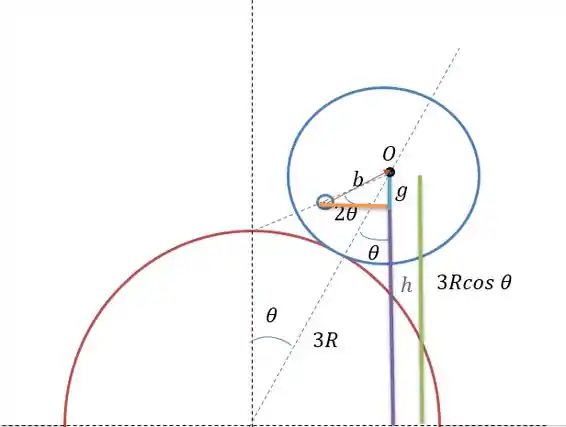
Sabemos que a distância do seu centro de massa até o centro da esfera de alumínio é de logo se rebateremos essa distância na vertical e tirarmos da distância vertical do alumínio teremos a sua altura em relação a , tal que.
Logo:
Então sua energia potencial gravitacional será:
Então a somatória das energias potencias das esferas será:
Passo 4
A derivada em relação a da energia do sistema será igual a:
O que diz que o sistema será equilibrado para .
Se derivarmos mais uma vez teremos:
Onde para o sistema será estável em:
Como o sistema é estável em logo o menor que devemos ter é: