Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 76

76- Determine o ângulo θ para haver equilíbrio da conexão uniforme de 10   k g e centro de massa em G , a medida que sua posição no plano vertical é influenciada pela força horizontal de 80   N aplicada a sua extremidade. A mola tem uma constante de 1.5   k N / m e não está alongada quando θ = 0 .

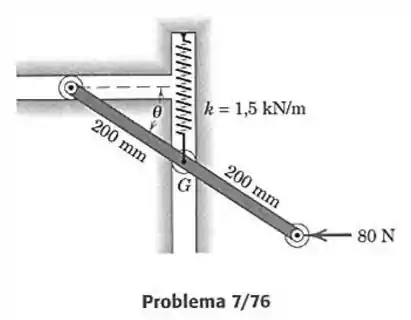
Passo 1

Vamos traçar nossos eixos de energia potencial nula e a partir dela calcular nossas energias potencial elástica e gravitacional.

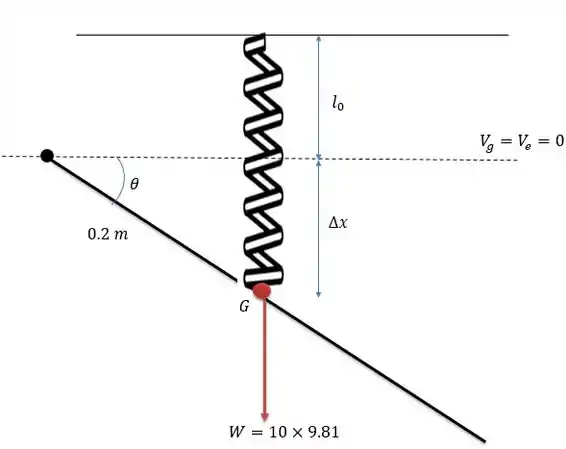
Como para θ = 0 não temos variação da energia potencial elástica e nem da potencial gravitacional logo nosso Δ x será igual ao h do centro de gravidade da barra. Tal que:

sin ⁡ θ = Δ x 0.2 → Δ x = h = 0.2 sin ⁡ θ

Logo a energia potencial gravitacional do sistema será:

V g = - m g h = 10 × 9.81 × 0.2 s i n θ = - 19.62 sin ⁡ θ

Não se esquecendo do fato do nosso centro de gravidade estar abaixo da linha nula, ficando negativa.

Agora a energia potencial elástica.

V e = 1 2 k   Δ x 2

Como k = 1.5   k N / m

V e = 1500 2   0.2 s i n θ 2 = 30 sin 2 ⁡ θ

Logo a energia potencial total do sistema será:

V = 30 sin 2 ⁡ θ - 19.62 sin ⁡ θ

Passo 2

Agora devemos nos preocupar com a força de 80   N que atua externamente ao sistema, pois ela fará trabalho efetivo no sistema. Tal que:

d V d θ = d U d θ

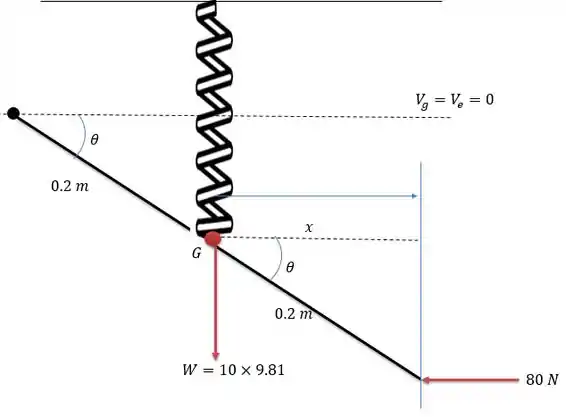
Essa força de 80   N gerará um trabalho no sistema igual a:

U = 80 x

Onde x será igual a:

cos ⁡ θ = x 0.2 → x = 0.2 cos ⁡ θ

Logo o trabalho será igual a:

U = - 80 × 0.2 cos ⁡ θ = - 16 cos ⁡ θ

Passo 3

Derivando a equação de energia do passo anterior e igualando com o trabalho feito pela força externa nós teremos:

d U d θ = d V d θ

16 s in ⁡ θ = 2 × 30 sin ⁡ θ cos ⁡ θ - 19.62 cos ⁡ θ

A solução é resolver numericamente ou plotar o gráfico de:

d V d θ = 16 sin ⁡ θ - 60 sin ⁡ θ cos ⁡ θ + 19.62 cos ⁡ θ

E ver quando essa função será zero.

Plotando então com intervalo de 0 ≤ θ ≤ 90 temos as seguintes posições de equilíbrio.

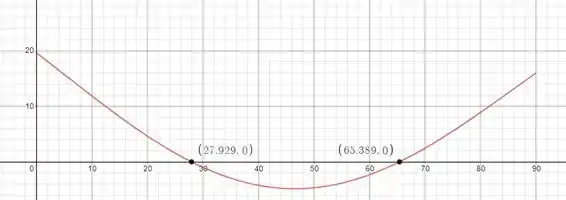
Encontramos θ = 27.93 ° e θ = 65.39 °

Resposta

θ = 27.93 °

θ = 65.39 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Especifique a força horizontal F necessária para manter o equilíbrio da plataforma de 80 kg em função do ângulo θ feito pelas barras de sustentação em relação à horizontal. Cada uma das três barras un
Ao se testar o projeto mostrado de um macaco guiado por um fuso, 12 voltas na manivela são necessárias para elevar o pedal de 24 mm. Se uma força F = 50 N, aplicada normalmente ao eixo da manivelam é
Calcule a eficiência com a qual a cunha, com inclinação de 5°, eleva o peso W , sob a ação da força horizontal P atuando na cunha. O coeficiente de atrito entre a cunha e o bloco vale 0,30.
A plataforma de trabalho portátil é elevada por intermédio de dois cilindros hidráulicos articulados nos pontos C . Cada cilindro está sob uma pressão hidráulica p e tem uma área de pistão A . Determi
A caçamba do caminhão de entrega de alimentos para aeronaves tem massa m quando carregada e é levantada pela aplicação de um torque M na extremidade inferior da engrenagem, que é articulada com a estr